Was ist eine Tangente?
Eine
Tangente ist eine Gerade, die etwas nur berührt, aber nicht schneidet. Legt man zum Beispiel eine Kugel auf ein glattes Brett, so berührt das Brett die Kugel ja nur, schneidet aber nichts aus ihr heraus. Das Brett wäre also eine Tangente an die Kugel.
Hier schnell zwei Beispiele:
Die grüne Gerade ist keine Tangente, da sie den Graphen schneidet, nicht nur berührt. Die rote Gerade ist eine Tangente, da sie den Graphen nur in einem Punkt berührt, ohne ihn zu schneiden.
Vorsicht, Sonderfall: Eine Tangente in einem
Wendepunkt durchquert den Funktionsgraphen sehr wohl. Trotzdem ist die rote Gerade offenbar die Tangente im Punkt (0|0), da sie die gleiche Steigung wie die Gerade hat.
Noch zu beachten: Eine Gerade, die in einem Punkt Tangente ist, darf den Graphen in einem anderen Punkt sehr wohl schneiden.
Wieso sucht man Tangenten von Funktionsgraphen?
Findet man eine Tangente an einen Funktionsgraphen in einem Punkt, dann kann man sagen, dass der Graph in dem Punkt die gleiche Steigung hat wie die Tangente. Also verwendet man Tangenten oft, um gut über die Steigung eines Funktionsgraphen reden zu können.
Wie kann man eine Tangente berechnen?
Wenn man die Tangente an der Stelle x finden will, tut man drei Sachen:
- x in die Funktion einsetzen, dann erhält man schon mal den Punkt, an dem die Tangente berührt
- x in die Ableitung einsetzen, dann erhält man die Steigung m der Tangente
- m und den obigen Punkt in die Geradengleichung
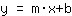 einseten, dann erhält man b.
einseten, dann erhält man b.
Kann ich dazu mal ein Beispiel sehen?
Ja, kannst du. So berechnet man die Tangente an die Funktion f(x)=x^3-2x für x=2.
Deine Eingabe: Funktion
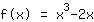
und Punkt 2
Wert 2 in
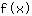
einsetzen:
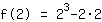 | | |
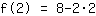 | | ( Rechne 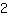 hoch hoch 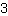 aus. ) aus. ) |
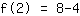 | | ( Multipliziere 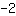 und und 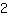 ) ) |
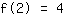 | | ( addiere  und und 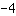 ) ) |
Also lautet der Punkt (2|4).
Allgemeine Funktion der Tangenten: y=mx+b mit m Steigung, b y-Achsenabschnitt.Steigung im Punkt (2|4) berechnen.
Dazu x-Koordinate in die Ableitungsfunktion von
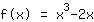
einsetzen.
| ( Ableitung von  ) + ( Ableitung von ) + ( Ableitung von 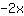 ) ) | | Die Ableitung von 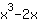 ist also ist also 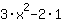 . . | |
Die Ableitung von
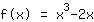
ist also
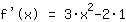
2 in
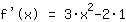
einsetzen:
Wert 2 in
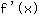
einsetzen:
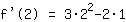 | | |
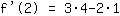 | | ( Rechne 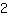 hoch hoch 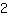 aus. ) aus. ) |
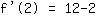 | | ( Multipliziere 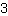 und und 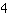 ) ) |
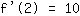 | | ( addiere 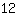 und und 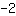 ) ) |
Also Tangente: y=10x+bb herausfinden: Punkt (2|4) in die Tangente einsetzen.
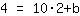 | | |
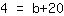 | | ( Multipliziere 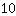 und und 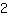 ) ) |
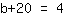 | | ( Vertausche beide Seiten der Gleichung. ) |
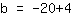 | | ( Bringe 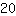 negativ auf die andere Seite. ) negativ auf die andere Seite. ) |
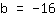 | | ( addiere 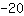 und und 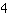 ) ) |
Also ist der y-Achsenabschnitt gleich -16
Tangente also: 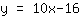
Kann ich noch mehr Beispiele sehen?
Klar, gib deine eigenen Beispiele einfach oben ein und sie werden dir sofort kostenlos genauso ausgerechnet.