What is a tangent line?
A tangent line is a line that just touches something without intersecting it. For example, if you put a ball on the ground, it does just touch the ground, but does not intersect it. So the ground would be a tangent to the ball.
Here are two examples:
The green line is no tangent cause the line intersects the graph without just touching it. The read line is a tangent cause it just touches the graph in one point without intersecting it.
Mind the special case: A tangent line in an ininflection point does cross the graph of the function. Anyway, the red line is obviously the tangent in the point (0|0), having the same slope as the graph.
Also think about this: A line being tangent in one point may very well intersect the graph in some other point.
Why should I search tangents of function graphs?
If you find a tangent to a graph in a point, you can say that the graph has the same slope as the tangent. So tangents are used to be able to talk about the slope of a graph.
How to calculate a tangent?
If you want to find the tangent on the point x, you do three things:
- Insert x into the function, so you got the point where the tangent touches
- Insert x into the derivation, so you got the slope m of the tangent.
- Insert m and the point into
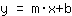, then you got b
Can I see some examples?
Of course. Just enter your function and a point into our free calculator. The tangent will then be found step-by-step.