How to transform the graph of a function?
This depends on the direction you want to transoform. In general, transformations in y-direction are easier than transformations in x-direction, see below.
How to move a function in y-direction?
Just add the transformation you want to to. This is it. For example, lets
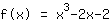
move this Graph by
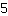
units to the top.
Your exercise:
The function 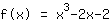 shall be moved by shall be moved by
5 to up
Graph before the transformation: :
|
|
Function after the transformation: 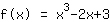
|
|
This is what Mathepower calculated:
Move the graph of 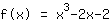 by 5 in direction up by 5 in direction up
Add 5 to the function.
Moved function: 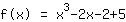
Simplify the new function: :
|
How to move a function in x-direction?
If you want to move in x-direction, it is more difficult for two reasons:
- You have to replace every x by
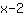
- and mind the sign: If you want to go in x-direction, replace x by
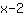 . But if you want to go in the opposite direction, you replace x by
. But if you want to go in the opposite direction, you replace x by  .
.
Here is another example involving the latter function.
Your exercise:
The function 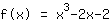 shall be moved by shall be moved by
2 to the right
Graph before the transformation: :
|
|
Function after the transformation: 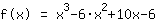
|
|
This is what Mathepower calculated:
Move the graph of 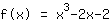 by 2 in direction right : by 2 in direction right :
Replace every x by 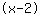
Moved function: 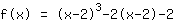
Simplify the new function: :
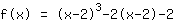 | | | Apply the higher binomial formula 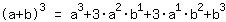 with a= with a= and b= and b=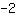 |
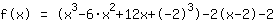 | | | Calculate 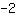 to the power of to the power of 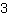 . . |
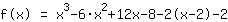 | | | Expand 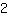 and and 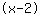 . . |
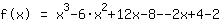 | | |
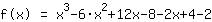 | | | add 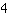 to to 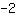 |
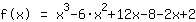 | | | add 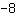 to to 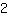 |
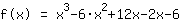 | | | add 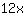 to to 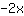 |
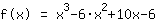 | | |
|
How to stretch a function in y-direction?
This is easy, again: Just multiply your whole function by the stretching factor. For example, lets stretch
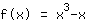
by Factor
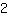
in y-direction.
Your exercise:
The function 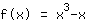 shall be moved by shall be moved by
2 in y-direction stretched
Graph before the transformation: :
|
|
Function after the transformation: 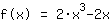
|
|
This is what Mathepower calculated:
Transform the function 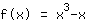 by 2 in y-direction stretch : by 2 in y-direction stretch :
Multiply the function by 2
Stretched function 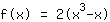
Simplify the new function: :
|
How to stretch a function in x-direction?
Again, like moving, stretchig is more difficult: We have to replace every x by
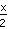
(Mind that it is again not the way you may think: Stretching does not mean multiplying by
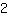
, but dividing by
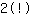
Your exercise:
The function 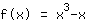 shall be moved by shall be moved by
2 in x-direction stretched
Graph before the transformation: :
|
|
Function after the transformation: 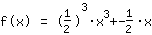
|
|
This is what Mathepower calculated:
Transform the function 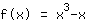 by 2 in x-direction stretch : by 2 in x-direction stretch :
Replace every x by 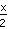
Stretched function 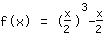
Simplify the new function: :
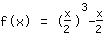 | | | Extract 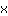 from the fraction from the fraction |
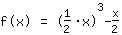 | | | Solve with the power laws : 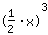 equals equals 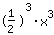 |
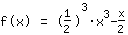 | | | Extract 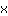 from the fraction from the fraction |
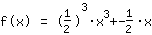 | | |
|
And if I want to move another function?
This is Mathepower. Just enter it above.