¿Qué es un estudio de una función?
Estudiar una función es poder determinar aspectos claves de una función como las raíces, la intersección en Y los puntos máximos y mínimos y los puntos de inflexión.
Mathepower te calcula todo con explicación paso a paso y gráfica de la función.
¿Cómo se determina estos puntos?
Determinando sus derivadas. Y luego pones la función así como sus derivadas igual a cero: Las raíces son soluciones de la ecuación.
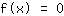
. Extremos solo pueden encontrarse en las raíces de la derivación p. ej. tienes que resolver la ecuación
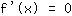
para determinar posibles extremos. (si se encuentran o no se encuentran extremos en las raíces de la derivación se puede comprobar mediante la regla de cambio de signos.) En un punto de inflexión la segunda derivación tiene que ser
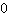
, entonces para determinar puntos de inflexión tienes que resolver la ecuación
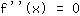
.
¿Por qué hoy en día ya no se realiza tanto el estudio de una función?
Porque no hace mucho sentido: Solo tienes que aprender una manera de hacer cada vez immer ;el mismo cálculo sobre puntos, sin pensar demasiado sobre su sentido. Por lo tanto los ejercicios que te hacen pensar sobre el sentido de los puntos tienen más importancia hoy en día.
¿Puedo ver un ejemplo?
Por supuesto. Echamos un vistazo al estudio de una función.

.
Mathepower calcula con esta función:
Aquí ves la gráfica de tu función.
|
|
- Raíces en -1; 0; 1
- Intersección en Y en (0|0)
- Puntos máximos y mínimos en (-0.577|0.385); (0.577|-0.385)
- Puntos de inflexión en (0|0)
Mathepower calculó lo siguiente:
Raíces:
Buscando raíces de 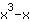
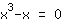 | | | Excluye  . . |
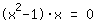 | | | 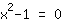 | | | El producto es 0. Entonces o el factor 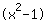 es cero es cero
|
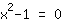 | | | +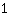 |
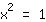 | | | Saca la raíz cuadrada en ambos lados. |
 | | |  | | | Calcula la raíz cuadrada de 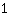 |
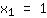 | | |  | | | Calcula la raíz cuadrada de 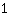 |
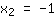 | | | 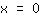 | | |
o bien el factor  es cero es cero |
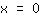 | | |
Entonces,las raíces son: {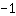 ; ;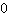 ; ;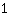 } }
Simetría:
 es simétrico respecto al punto O. es simétrico respecto al punto O.
insertar
Introduce 0 en la función 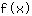 : :
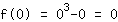
Entonces,la intersección en Y es en (0|0)
Derivada de una función 
| Deriva la función 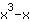 : : | ( Derivada de  ) ) | + | ( Derivada de 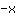 ) ) | 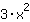 | + | 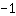 |
Entonces,la derivada de 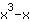 es es 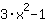 . . |
| |
|
Entonces la primera derivada es 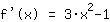
Segunda derivada,por ejemplo: derivada de 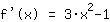 : :
| Deriva la función 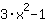 : : | ( Derivada de 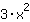 ) ) | + | ( Derivada de 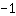 ) ) | 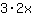 | + | 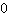 |
Entonces,la derivada de 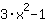 es es 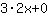 . . |
| |
|
Simplificar derivadas:
Entonces la segunda derivada es 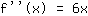
Tercera derivada,por ejemplo: derivada de 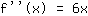 : :
La derivada de 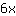 es es 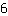
Entonces la tercera derivada es 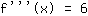
Buscando puntos extremos
Tenemos que encontrar las raíces de la primera derivada.
Buscando raíces de 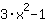
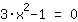 | | | +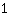 |
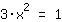 | | | : 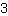 |
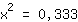 | | | Saca la raíz cuadrada en ambos lados. |
 | | |  | | | Calcula la raíz cuadrada de  |
 | | |  | | | Calcula la raíz cuadrada de  |
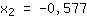 | | |
Posibles extremos en {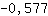 ; ;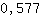 } }
Pon las raíces de la primera derivada dentro de la segunda:
Introduce -0.577 en la función 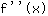 : :
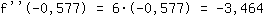
-3.464 es menor que 0. Entonces hay un máximo en 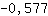 . .
Introduce -0.577 en la función 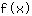 : :
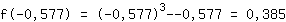
Punto máximo (-0.577|0.385)
Introduce 0.577 en la función 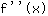 : :

3.464 es mayor que 0. Entonces hay un mínimo en 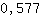 . .
Introduce 0.577 en la función 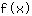 : :
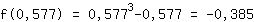
Punto mínimo (0.577|-0.385)
Buscando puntos de inflexión.
Tenemos que encontar las raíces de la segunda derivada.
Buscando raíces de 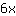
Puntos de inflexión podrían ser en {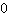 } }
Pon las raíces de la segunda derivada en la tercera derivada:
La tercera derivada no tiene x ,entonces el resultado de la inserción es 6
6 es mayor que 0,entonces hay un punto de inflexión en 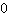 . .
Introduce 0 en la función 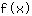 : :
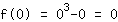
Punto de inflexión (0|0)
|