Reconstrucción de funciones


Reconstruir una ecuación: Introduce raíces, puntos de inflexión, extremos o otros puntos que conoces, Mathepower calcula la función que pasa por ellos y te da la gráfica correspondiente.

Grado de la función:
1 2 3 4 5

( El grado es el exponente más alto detrás de un x. )


Simetrías:
simetría axial respecto al eje Y
simetría central respecto al origen


Intersección en Y



Raíces / puntos máximos / puntos mínimos / puntos de inflexión:
en x=
en x=
en x=
en x=
en x=


Puntos característicos:
en |)
en |)
en |)
en (|)
en (|)


Pendiente en coordenadas x dados:
Pendiente en x=
Pendiente en x=
Pendiente en

¿En qué consiste la reconstrucción de funciones?

Es de alguna manera,lo contrario de un estudio de una función. El estudio de una función quiere decir que tienes una función y quieres determinar sus raíces, sus extremos y sus puntos de inflexión. Lo que hacemos aquí es el contrario: Tenemos unas raíces, unos puntos de inflexión, unos extremos etc. y estamos buscando una función que contiene todos estos valores.

¿Cómo se reconstruye una función?

Principalmente, tienes que encontrar ecuaciones y resolverlas. De esta manera recibes los coeficientes de tu función. Aquí tienes un ejemplo: Asumamos que estamos buscando una función de tercer grado con un mínimo en (1|-4) y un máximo en (-1|3).


Estás buscando una función con:
función cuadrática
Punto máximo en (-1|3)
Punto mínimo en (1|-4)

Mathepower encontró la siguiente función:
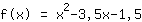
1*f(x)=1*x^2+-3.5*x+-1.5
Aquí ves la gráfica de tu función.
Dein Browser untersttzt den HTML-Canvas-Tag nicht. Hol dir einen neuen. :P
  • Raíces en -0.386; 3.886
  • Intersección en Y en (0|-1.5)
  • Puntos máximos y mínimos en (1.75|-4.563)
  • Puntos de inflexión

Así calculó Mathepower:
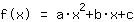
f(x)=1*a*x^2+1*b*x+1*c
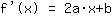
f'(x)=2*a*x+1*b
f''(x)=2*a

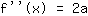
El punto en (-1|3) da la ecuación :
f(-1)=3
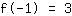
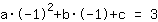
1*a*-1^2+1*b*-1+1*c=3
simplificado: :
1a-1b+1c=3

El punto en (1|-4) da la ecuación :
f(1)=-4
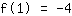
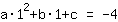
1*a*1^2+1*b*1+1*c=-4
simplificado: :
1a+1b+1c=-4

Asi,tenemos el siguiente sistema de ecuaciones: :
  a   -1b   +c    = 3 
  a   +b   +c    = -4 

Así resolvemos este sistema de ecuaciones:
  a   -1b   +c    = 3 
  a   +b   +c    = -4 
  a   -1b   +c    = 3 
     2b       = -7 
 ( -1 veces de la fila 1 se añade a la fila 2 )
  a   -1b   +c    = 3 
     b       = -3,5 
 ( fila 2 fue dividida por 2 )

2 fila: b+0c = -3,5
c puedes elegir libremente
Resuelve para b : :   b = 0c -3,5

1 fila:
a  -1b  +c   =  3
Introduce las variables ya conocidas:   
a  -1⋅(0c -3,5)  +⋅1c    =  3
Resuelve para a : a = -1c -0,5
Pon a egual
Eso significa que c es -1,5

Insertando demuestra que la función es igual a 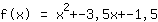f(x)=1*1*x^2+1*-3.5*x+1*-1.5 ist.



¿Cómo hallar una función conociendo sus puntos?

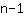
La regla general es que por cada n puntos dados hay una función del grado n-1 cuya gráfica pasa por ellos. Entonces resolviendo ecuaciones encuentras una función de tercer grado que pasa por los siguiente cuatro puntos (-1|3),(0|2),(1|1) y (2|4):


Estás buscando una función con:
función del grado 3
Punto en (-1|3)
Punto en (0|2)
Punto en (1|1)
Punto en (2|4)

Mathepower encontró la siguiente función:
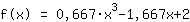
1*f(x)=0.667*x^3+-1.667*x+2
Aquí ves la gráfica de tu función.
Dein Browser untersttzt den HTML-Canvas-Tag nicht. Hol dir einen neuen. :P
  • Raíces en -2
  • Intersección en Y en (0|2)
  • Puntos máximos y mínimos en (-0.913|3.014); (0.913|0.986)
  • Puntos de inflexión en (0|2)

Así calculó Mathepower:
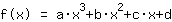
f(x)=1*a*x^3+1*b*x^2+1*c*x+1*d
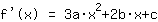
f'(x)=3*a*x^2+2*b*x+1*c
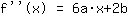
f''(x)=6*a*x+2*b

El punto en (-1|3) da la ecuación :
f(-1)=3
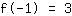
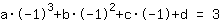
1*a*-1^3+1*b*-1^2+1*c*-1+1*d=3
simplificado: :
-1a+1b-1c+1d=3

El punto en (0|2) da la ecuación :
f(0)=2
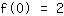
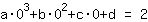
1*a*0^3+1*b*0^2+1*c*0+1*d=2
simplificado: :
0a+0b+0c+1d=2

El punto en (1|1) da la ecuación :
f(1)=1
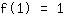
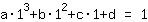
1*a*1^3+1*b*1^2+1*c*1+1*d=1
simplificado: :
1a+1b+1c+1d=1

El punto en (2|4) da la ecuación :
f(2)=4
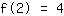
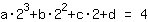
1*a*2^3+1*b*2^2+1*c*2+1*d=4
simplificado: :
8a+4b+2c+1d=4

Asi,tenemos el siguiente sistema de ecuaciones: :
  -1a   +b   -1c   +d    = 3 
           d    = 2 
  a   +b   +c   +d    = 1 
  8a   +4b   +2c   +d    = 4 

Así resolvemos este sistema de ecuaciones:
  -1a   +b   -1c   +d    = 3 
           d    = 2 
  a   +b   +c   +d    = 1 
  8a   +4b   +2c   +d    = 4 
  -1a   +b   -1c   +d    = 3 
           d    = 2 
  a   +b   +c   +d    = 1 
     -4b   -6c   -7d    = -4 
 ( -8 veces de la fila 3 se añade a la fila 4 )
  -1a   +b   -1c   +d    = 3 
           d    = 2 
     2b      +2d    = 4 
     -4b   -6c   -7d    = -4 
 ( 1 veces de la fila 1 se añade a la fila 3 )
  a   -1b   +c   -1d    = -3 
           d    = 2 
     2b      +2d    = 4 
     -4b   -6c   -7d    = -4 
 ( fila 1 fue dividida por -1 )
  a   -1b   +c   -1d    = -3 
           d    = 2 
     2b      +2d    = 4 
        -6c   -3d    = 4 
 ( 2 veces de la fila 3 se añade a la fila 4 )
  a   -1b   +c   -1d    = -3 
     2b      +2d    = 4 
           d    = 2 
        -6c   -3d    = 4 
 ( fila 3 fue intercambiada por la fila 2 )
  a   -1b   +c   -1d    = -3 
     b      +d    = 2 
           d    = 2 
        -6c   -3d    = 4 
 ( fila 2 fue dividida por 2 )
  a   -1b   +c   -1d    = -3 
     b      +d    = 2 
        -6c   -3d    = 4 
           d    = 2 
 ( fila 4 fue intercambiada por la fila 3 )
  a   -1b   +c   -1d    = -3 
     b      +d    = 2 
        c   +0,5d    = -0,667 
           d    = 2 
 ( fila 3 fue dividida por -6 )


4 fila:
      d   =  2

3 fila:
    c  +0,5d   =  -0,667
Introduce las variables ya conocidas:   
    c  +0,5⋅2   =  -0,667
Resuelve para c : c = -1,667

2 fila:
  b    +d   =  2
Introduce las variables ya conocidas:   
  b    +⋅2   =  2
Resuelve para b : b = 0

1 fila:
a  -1b  +c  -1d   =  -3
Introduce las variables ya conocidas:   
a  -1⋅0  +⋅(-1,667)  -1⋅2   =  -3
Resuelve para a : a = 0,667

Insertando demuestra que la función es igual a 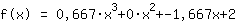f(x)=1*0.667*x^3+1*0*x^2+1*-1.667*x+1*2 ist.



¿Cómo hallar una función conociendo sus puntos de inflexión?

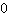
Un punto de inflexión da varias ecuaciones: Por un lado, tienes el valor Y, por otro lado sabes que la segunda derivada en un punto de inflexión es 0. Dejanos mirar un ejemplo de una función de tercer grado que tiene un punto de inflexión en (1|3):


Estás buscando una función con:
función del grado 3
Raíces en 2
Raíces en 4
Punto de inflexión en (1|3)

Mathepower encontró la siguiente función:
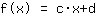
1*f(x)=1*c*x+1*d
Aquí ves la gráfica de tu función.
Dein Browser untersttzt den HTML-Canvas-Tag nicht. Hol dir einen neuen. :P
  • Raíces
  • Intersección en Y en (0|0)
  • Puntos máximos y mínimos
  • Puntos de inflexión

Así calculó Mathepower:
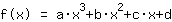
f(x)=1*a*x^3+1*b*x^2+1*c*x+1*d
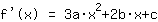
f'(x)=3*a*x^2+2*b*x+1*c
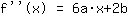
f''(x)=6*a*x+2*b

El punto en (1|3) da la ecuación :
f(1)=3
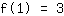
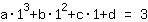
1*a*1^3+1*b*1^2+1*c*1+1*d=3
simplificado: :
1a+1b+1c+1d=3

Asi,tenemos el siguiente sistema de ecuaciones: :
  a   +b   +c   +d    = 3 

Así resolvemos este sistema de ecuaciones:
  a   +b   +c   +d    = 3 

1 fila: c+1d = 3
d puedes elegir libremente
Resuelve para c : :   c = -1d +3

Insertando demuestra que la función es igual a 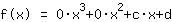f(x)=1*0*x^3+1*0*x^2+1*c*x+1*d ist.



¿Y cómo puedo aplicar todo esto a un ejemplo mío?

Sólo introduce tu tarea en el campo arriba. Mathepower te demuestra cómo hacerlo mediante un cálculo paso a paso y gratuito. O simplemente invéntate cualquier tarea interesante y verás como Mathepower la puede resolver.