Encontrando as funções


Encontre uma função

Grau da função:
1 2 3 4 5

( O grau é o maior expoente de x )


Simetrias:
eixo simétrico ao eixo-y
ponto simétrico á origem


intercepção do eixo-y



Raízes / Máximas / Mínimas / Pontos de inflexão:
á x=
á x=
á x=
á x=
á x=


Pontos característicos:
á |)
á |)
á |)
á (|)
á (|)


Inclinação dada na coordenada x:
Inclinação á x=
Inclinação á x=
Inclinação á

O que é isso?

Isto, de qlguma forma é o oposto do esboço de curva. No esboço de curva você tem uma função e está procurando pela raíz, pontos extremos e de inflexão. O que deve ser feito aqui é o oposto: Você tem as raízes, pontos extremos e de inflexão e procuura pelas suas funções.

Como resconstruir uma função?

Primeiro, você deve encontrar as equações e reolvê-las. Isso te dará os coeficientes da sua função. Exemplo: Assumindo que estamos olhando para uma função de 3° grau tendo um ponto extremo mínimo em (1|-4) e máximo em (-1|3).


Você está procurando uma função com:
função quadrática
Ponto extremo máximo á (-1|3)
Ponto extremo mínimo á (1|-4)

Mathepower encontrou a seguinte função:
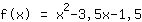
1*f(x)=1*x^2+-3.5*x+-1.5
Aqui está o gráfico da sua função.
Dein Browser unterstützt den HTML-Canvas-Tag nicht. Hol dir einen neuen. :P
  • Raízes á -0.386; 3.886
  • intercepção do eixo-y á (0|-1.5)
  • Mais alto e mais baixo ponto extremo á (1.75|-4.563)
  • Pontos de inflexão

Assim a Mathepower calcula:
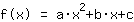
f(x)=1*a*x^2+1*b*x+1*c
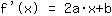
f'(x)=2*a*x+1*b
f''(x)=2*a

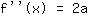
O ponto em (-1|3) dá a equação :
f(-1)=3
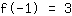
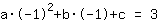
1*a*-1^2+1*b*-1+1*c=3
simplificada: :
1a-1b+1c=3

O ponto em (1|-4) dá a equação :
f(1)=-4
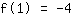
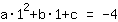
1*a*1^2+1*b*1+1*c=-4
simplificada: :
1a+1b+1c=-4

Então, temos os seguintes sistemas de equação: :
  a   -1b   +c    = 3 
  a   +b   +c    = -4 

O sistema de equações é resolvido da seguinte forma:
  a   -1b   +c    = 3 
  a   +b   +c    = -4 
  a   -1b   +c    = 3 
     2b       = -7 
 ( -1 1 Foi adicionada á linha 2 )
  a   -1b   +c    = 3 
     b       = -3,5 
 ( a 2 linha foi dividida 2 )

2 linha: b+0c = -3,5
c pode ser livremente escolhido
Resolva b : :   b = 0c -3,5

1 linha:
a  -1b  +c   =  3
Use as variáveis já calculadas:   
a  -1⋅(0c -3,5)  +⋅1c    =  3
Resolva a : a = -1c -0,5
Defina a igual a
Significa que c é igual a -1,5

A inserção mostra que as funções são iguais 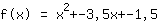f(x)=1*1*x^2+1*-3.5*x+1*-1.5 ist.



Como encontro a função através desses pontos?

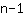
A regra geral é que para qualquer n ponto dado existe uma função de grau n-1 cujo gráfico passa por eles. Então você pode encontrar reolvendo uma função de 3° grau através de quatro pontos (-1|3), (0|2), (1|1) e (2|4):


Você está procurando uma função com:
função do grau 3
Ponto á (-1|3)
Ponto á (0|2)
Ponto á (1|1)
Ponto á (2|4)

Mathepower encontrou a seguinte função:
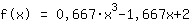
1*f(x)=0.667*x^3+-1.667*x+2
Aqui está o gráfico da sua função.
Dein Browser unterstützt den HTML-Canvas-Tag nicht. Hol dir einen neuen. :P
  • Raízes á -2
  • intercepção do eixo-y á (0|2)
  • Mais alto e mais baixo ponto extremo á (-0.913|3.014); (0.913|0.986)
  • Pontos de inflexão á (0|2)

Assim a Mathepower calcula:
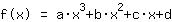
f(x)=1*a*x^3+1*b*x^2+1*c*x+1*d
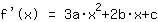
f'(x)=3*a*x^2+2*b*x+1*c
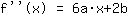
f''(x)=6*a*x+2*b

O ponto em (-1|3) dá a equação :
f(-1)=3
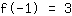
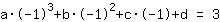
1*a*-1^3+1*b*-1^2+1*c*-1+1*d=3
simplificada: :
-1a+1b-1c+1d=3

O ponto em (0|2) dá a equação :
f(0)=2
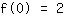
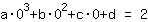
1*a*0^3+1*b*0^2+1*c*0+1*d=2
simplificada: :
0a+0b+0c+1d=2

O ponto em (1|1) dá a equação :
f(1)=1
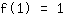
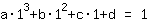
1*a*1^3+1*b*1^2+1*c*1+1*d=1
simplificada: :
1a+1b+1c+1d=1

O ponto em (2|4) dá a equação :
f(2)=4
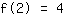
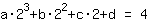
1*a*2^3+1*b*2^2+1*c*2+1*d=4
simplificada: :
8a+4b+2c+1d=4

Então, temos os seguintes sistemas de equação: :
  -1a   +b   -1c   +d    = 3 
           d    = 2 
  a   +b   +c   +d    = 1 
  8a   +4b   +2c   +d    = 4 

O sistema de equações é resolvido da seguinte forma:
  -1a   +b   -1c   +d    = 3 
           d    = 2 
  a   +b   +c   +d    = 1 
  8a   +4b   +2c   +d    = 4 
  -1a   +b   -1c   +d    = 3 
           d    = 2 
  a   +b   +c   +d    = 1 
     -4b   -6c   -7d    = -4 
 ( -8 3 Foi adicionada á linha 4 )
  -1a   +b   -1c   +d    = 3 
           d    = 2 
     2b      +2d    = 4 
     -4b   -6c   -7d    = -4 
 ( 1 1 Foi adicionada á linha 3 )
  a   -1b   +c   -1d    = -3 
           d    = 2 
     2b      +2d    = 4 
     -4b   -6c   -7d    = -4 
 ( a 1 linha foi dividida -1 )
  a   -1b   +c   -1d    = -3 
           d    = 2 
     2b      +2d    = 4 
        -6c   -3d    = 4 
 ( 2 3 Foi adicionada á linha 4 )
  a   -1b   +c   -1d    = -3 
     2b      +2d    = 4 
           d    = 2 
        -6c   -3d    = 4 
 ( a 3 linha foi trocada com 2 linha )
  a   -1b   +c   -1d    = -3 
     b      +d    = 2 
           d    = 2 
        -6c   -3d    = 4 
 ( a 2 linha foi dividida 2 )
  a   -1b   +c   -1d    = -3 
     b      +d    = 2 
        -6c   -3d    = 4 
           d    = 2 
 ( a 4 linha foi trocada com 3 linha )
  a   -1b   +c   -1d    = -3 
     b      +d    = 2 
        c   +0,5d    = -0,667 
           d    = 2 
 ( a 3 linha foi dividida -6 )


4 linha:
      d   =  2

3 linha:
    c  +0,5d   =  -0,667
Use as variáveis já calculadas:   
    c  +0,5⋅2   =  -0,667
Resolva c : c = -1,667

2 linha:
  b    +d   =  2
Use as variáveis já calculadas:   
  b    +⋅2   =  2
Resolva b : b = 0

1 linha:
a  -1b  +c  -1d   =  -3
Use as variáveis já calculadas:   
a  -1⋅0  +⋅(-1,667)  -1⋅2   =  -3
Resolva a : a = 0,667

A inserção mostra que as funções são iguais 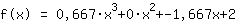f(x)=1*0.667*x^3+1*0*x^2+1*-1.667*x+1*2 ist.



Como encontrar a função através de um ponto de inflexão?

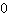
Um ponto de inflexão te dá multiplas equações: Por um lado, você tem valor-y. Do outro, você sabe que a segunda derivada é 0 em um ponto de inflexão. Vejamos um exemplo para uma função de 3°grau que contenha um ponto de inflexão em (1|3):


Você está procurando uma função com:
função do grau 3
raíz á 2
raíz á 4
Ponto de inflexão á (1|3)

Mathepower encontrou a seguinte função:
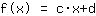
1*f(x)=1*c*x+1*d
Aqui está o gráfico da sua função.
Dein Browser unterstützt den HTML-Canvas-Tag nicht. Hol dir einen neuen. :P
  • Raízes
  • intercepção do eixo-y á (0|0)
  • Mais alto e mais baixo ponto extremo
  • Pontos de inflexão

Assim a Mathepower calcula:
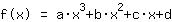
f(x)=1*a*x^3+1*b*x^2+1*c*x+1*d
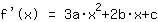
f'(x)=3*a*x^2+2*b*x+1*c
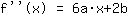
f''(x)=6*a*x+2*b

O ponto em (1|3) dá a equação :
f(1)=3
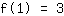
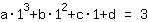
1*a*1^3+1*b*1^2+1*c*1+1*d=3
simplificada: :
1a+1b+1c+1d=3

Então, temos os seguintes sistemas de equação: :
  a   +b   +c   +d    = 3 

O sistema de equações é resolvido da seguinte forma:
  a   +b   +c   +d    = 3 

1 linha: c+1d = 3
d pode ser livremente escolhido
Resolva c : :   c = -1d +3

A inserção mostra que as funções são iguais 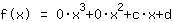f(x)=1*0*x^3+1*0*x^2+1*c*x+1*d ist.



E como uso isso no meu exemplo?

Basta inserir seu exercício acima. A Mathepower mostrará como funciona fazendo o cálculo passo a passo. Ou apenas faça um exercício qualquer e veja o que a Mathepower faz.