Como resolver uma equação linear básica?
Primeiro, veja esse exemplo:
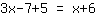
Primeiro, simplifique ambos os lados. Na esquerda some
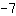
com
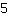
. Então temos a equação:
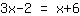
Agora você deve rearranjar a equação de um modo que x fique no lado esquerdo e os números fiquem do lado direito. Como não queremos x no lado direito, subtraimos x em ambos os lados.
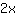
são colocados no lado esquerdo.
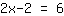
Agora, temos que colocar o
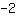
no outro lado. Então somamos
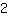
em ambos os lados.
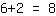
, e temos
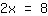
Então, dividimos ambos os lados pelo número a frente de x:
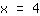
A equação está resolvida; a resposta é
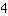
.
Você sempre pode proceder exatamente da mesma maneira: Primeiro, simplificar ao máximo ambos os lados da equação. Então, simplifique transformando com equivalência. Subtraia um número em ambos os lados. E finalmente, tendo as variáveis de um lado e os números de outro. Divida pelo número em frente a variável e a equação está resolvida.
Como a Mathepower mostra a solução?
Quando uma equação é inserida, você tem:
| Seu exercício: | | Passo a passo: |
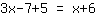 | | | Adicione 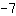 a a 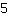 |
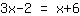 | | | 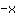 |
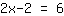 | | | +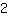 |
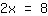 | | | : 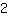 |
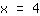 | | |
Conjunto solução: {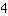 } } |
E se eu quiser resolver outra equação?
Você está na Mathepower.com. Insira sua equação e ela será resolvida nos mesmos procedimentos. De forma imediata e gratuita (mathepower é financiada por empresas privadas)
Existem casos especias a serem considerados em uma equação?
O mais importante caso é quando a equação não tem solução ou infinitas soluções.
Vejamos um exemplo de equação com infinitas soluções:
| Seu exercício: | | Passo a passo: |
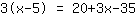 | | | Expanda 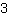 e e  . . |
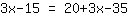 | | | Adicione 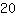 a a  |
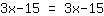 | | | 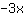 |
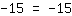 | | | | A equação é universalmente válida. |
|
Conjunto solução: R |
Quando você acaba com os mesmos números em ambos os lados da equação. (não existe mais x). Assim, vemos que uma equação pode ter um infinito número de soluções.
Mas o que significa ter infinitas soluções? Vamos supor: use qualquer valor para x (por exemplo,
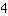
, ambos os lados serão iguais. Isso funciona com quelquer valor para x. A razão disso, é que os termos em ambos os lados são equivalentes, ou seja, termos com a mesma solução para qualquer valor em x.
Outro caso é uma equação sem solução:
| Seu exercício: | | Passo a passo: |
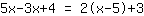 | | | Adicione 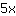 a a 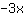 |
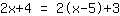 | | | Expanda 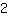 e e  . . |
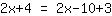 | | |
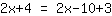 | | | Adicione 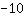 a a 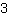 |
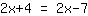 | | | 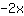 |
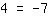 | | | | Não há resultado para esta equação . |
|
Conjunto solução: {} |
Quando vemos que não existe x depois de rearranjarmos a equação. Isso é devido á equação original não ter solução.