Forma vértice


Forma vértice

Insira a função a ser colocada na forma vértice.

Dica: Enter sendo 3*x^2.






O que é fórmula do vértice?

A fórmula do vértice é uma forma especial de uma função quadrática. A partir dela. É que podemos enxergar onde o ponto máximo ou mínimo (vértice) está: O número entre parênteses indica a coordenada-x do vértice, e o número ao final da fórmula te dá a coordenada-y.

Como colocar a função na fórmula do vértice?

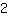
Você deve primeiro realizar o completamento do quadrado: Pegue o número em frente a x e divida por 2. Veja o exemplo:


Mathepower funciona com essa função:

Então, a vértice da sua função é 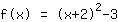f(x)=1*(x+2)^2+-3
O vértice está em (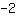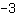-2|-3)

Aqui está o gráfico da sua função.
Dein Browser unterstützt den HTML-Canvas-Tag nicht. Hol dir einen neuen. :P
  • ponto vértice á (-2|-3)
Isto é o que a Mathepower calculou:
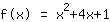f(x)=1*x^2+4*x+1
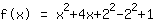f(x)=x^2+4*x+(2)^2+-1*(2)^2+1( Ao quadrado )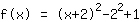
f(x)=(x+2)^2+-1*(2)^2+1( Use a fórmula binominal )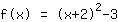
f(x)=(x+2)^2+-3( Simplifique )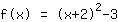
f(x)=1*(x+2)^2+-3( Expanda )

Como pode ver, a cooredenada-x do vértice é igual ao número em parênteses, mas apenas até atroca de sinais Portanto, vê-se neste cálculo que você precisa apenas usar a fórmula binomial para trás: construa uma fórmula binomial fora do termo da função. Isso funciona apenas se houver o número correto (que complete o quadrado). Então é so somá-lo e subtrai-lo a mesmo tempo.

E se houver um número na frente do x^2?

Então você deverá fatorizar esse número. Exemplo:


Mathepower funciona com essa função: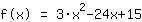
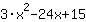=3*x^2+-1*24*x+15

Então, a vértice da sua função é 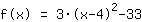f(x)=3*(x+-4)^2+-33
O vértice está em (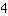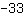4|-33)

Aqui está o gráfico da sua função.
Dein Browser unterstützt den HTML-Canvas-Tag nicht. Hol dir einen neuen. :P
  • ponto vértice á (4|-33)
Isto é o que a Mathepower calculou:
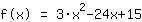f(x)=3*x^2+-24*x+15
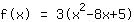f(x)=3*(x^2+-8*x+5)( Fatore )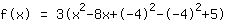
f(x)=3*(x^2+-8*x+(-4)^2+-1*(-4)^2+5)( Ao quadrado )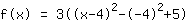
f(x)=3*((x+-4)^2+-1*(-4)^2+5)( Use a fórmula binominal )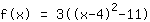
f(x)=3*((x+-4)^2+-11)( Simplifique )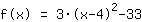
f(x)=3*(x+-4)^2+-33( Expanda )

É importante você primeiro fatorizar o número para depois realizar o completamento do quadrado. Caso contrário podem occorrer erros não muito agradáveis. (infelizmente muitas pessoas não pensam nisso e simplesmente usam a fórmula binomial mesmo náo sendo possível... Infelizmente o exercício não pode gritar ''OUCH'', mas os professores sim!

E caso haja um sinal de menos na frente de x^2?

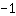
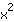
Apenas fatorize o -1. A propósito: sempre que houver um número negativo em x^2, a parábola é aberta para baixo. Exemplo:


Mathepower funciona com essa função: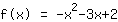
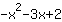=-1*x^2+-1*3*x+2

Então, a vértice da sua função é 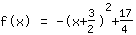f(x)=-1*(x+3/2)^2+17/4
O vértice está em (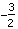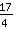-3/2|17/4)

Aqui está o gráfico da sua função.
Dein Browser unterstützt den HTML-Canvas-Tag nicht. Hol dir einen neuen. :P
  • ponto vértice á (-1.5|4.25)
Isto é o que a Mathepower calculou:
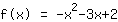f(x)=-1*x^2+-3*x+2
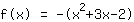f(x)=-1*(x^2+3*x+-2)( Fatore )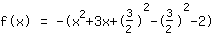
f(x)=-1*(x^2+3*x+(3/2)^2+-1*(3/2)^2+-2)( Ao quadrado )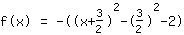
f(x)=-1*((x+3/2)^2+-1*(3/2)^2+-2)( Use a fórmula binominal )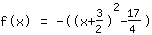
f(x)=-1*((x+3/2)^2+1*-17/4)( Simplifique )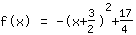
f(x)=-1*(x+3/2)^2+17/4( Expanda )

E qual a fórmula geral para o vértice?

É só inserir sua função que a Mathepower resolve f_f(x)=ax^2+bx+c .


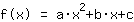
Mathepower funciona com essa função:

Então, a vértice da sua função é 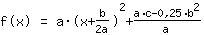f(x)=1*a*(x+b/(2*a))^2+(1*a*c+-0.25*b^2)/a
O vértice está em (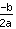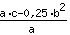(-1*b)/(2*a)|(1*a*c+-0.25*b^2)/a)

Isto é o que a Mathepower calculou:
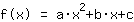f(x)=1*a*x^2+1*b*x+1*c
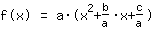f(x)=1*a*(x^2+b/a*x+c/a)( Fatore )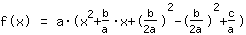
f(x)=1*a*(x^2+b/a*x+(b/(2*a))^2+-1*(b/(2*a))^2+c/a)( Ao quadrado )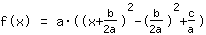
f(x)=1*a*((x+b/(2*a))^2+-1*(b/(2*a))^2+c/a)( Use a fórmula binominal )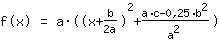
f(x)=1*a*((x+b/(2*a))^2+1*(1*a*c+-0.25*b^2)/a^2)( Simplifique )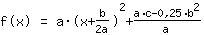
f(x)=1*a*(x+b/(2*a))^2+(1*a*c+-0.25*b^2)/a( Expanda )

Posso ver mais exemplos?

Claro. Esta é uma calculadora para fórmulas de vétice. Basta inserir seu exemplo e será resolvido imediatamente.