什么是导数？
函数在 x 处的导数表示了在 x 处函数的斜率，也就是说 在点 ( x|f(x) )处，函数切线的斜率数值。
例：正态抛物线
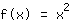
在点 (1|1)处的切线为 2x-1，即斜率为2。所以正态抛物线的导数 在
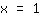
处等于2。
导数与导数函数的区别是什么？
函数 f(x) 的导数函数 f'(x) 是一个函数，它给出了在任意 x 值处的函数斜率。 这表示：如果要求函数在 x 处的斜率，只需要将 x 值代入导数函数 中。
如何计算导数呢？
在发现求导公式之前，人们必须要对每一点求单独求差商。 使用求导公式，一切就变得简单了：首先我们确定每一个幂函数的导数 。
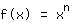
. 简单来说就是
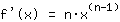
. 进一步使用公式计算任意多项式函数的导数 ，因为这仅仅就是幂函数求导结果与数字 的求和。为此，需要运用公式
对更复杂的函数来说，需要更多的求导规则：
- 乘积规则：函数
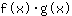的导数等于 
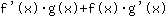
- 除法规则：函数
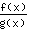的导数等于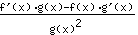 
- 链式规则：函数
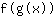的导数等于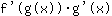 
为什么需要确定导数的零点？
导数零点是在函数图像绘制时重要的点。函数的最大极值点和最小极值点即为函数一阶导数的零点。 （注意！反过来，一阶导数的零点却并不一定是函数的极值点！详见符号变化相关规则） 在函数的拐点处，二阶导数为0。因此，我们可以通过求函数导数的零点 了解关于这个函数更多的信息。