在什么时候我们需要分数呢?
例如:想象有四个人分食一个蛋糕,每个人可以分到多少蛋糕呢?计算结果 当然就是 1:4。但这个结果什么呢? 答案是,单纯的创造出一个数字写作
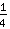
(读作:四分之一)。如果你想要想象 它有多大,只需要画一个蛋糕,然后将它分为四块。
这样的分数是什么呢?
我们刚刚对蛋糕所做的计算,也可以应用到每一个数字:想象我们需要两个数字进行除法,但无法整除。那么 那我们只需创造一个数字来代表这个结果。所以分数
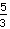
就仅仅表示 5:3的结果。在上方的数字叫做分子,下方的数字叫做分母。所以,
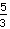
的分子为
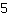
,分母为
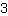
。
如何进行这些分数的计算呢?
首先记住:有许多看似不同的分数其实代表的是同一个数。例如,2/2 等于
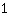
,
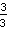
也等于 1, 因为
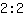
和
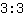
的结果都是
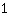
。所以我们就由两个看上去不同的分数来表述同一个数字。将一个分数 转化为表示相同数的另外一个分数,叫做分数的扩展或简化。
如果你想要进行分数的加减法,你需要将它们化为同分母的分数。这可以通过 寻找这两个分母的最小公倍数来实现。
如果想进行分数的乘法,需要将分子与分子相乘、分母与分母相乘。进行分数除法时, 需要将除数的分子和分母倒置,然后与被除数相乘。
含有分数的数域叫什么呢?
是有理数。