符号变化规则有什么用?
通过观察导数符号的变化,我们可以观察在函数导数为
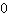
处的点是最大极值点、最小极值点还是鞍点。 这里有三个例子,方程在 (1|2)处的斜率为 0:
函数的斜率在 (1|2) 处斜率为 0,且是一个最大极值点。在
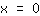
处,函数图像上升,也就是说函数导数在这里是大于 0。在

处, 函数图像下降,也就是说导数在这里小于
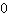
。这些说明,在函数的最大极值点附近,函数导数的符号变化为 先正(+)后负(-)。也即是导数值的符号从 + 变为 - 。
函数的斜率在 (1|2) 处斜率为 0,且是一个最小极值点。在
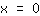
处,函数图像下降,也就是说函数导数在这里是小于 0。 在

处,函数图像上升,也就是说导数在这里大于
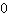
。这些说明,这个点是最小极值点。 函数导数的符号变化为先负(-)后正(+)。也即是导数值的符号 从 - 变为 +。
函数的斜率在 (1|2) 处斜率仍然为 0,但它并不是极值点。可以从图像中看出 函数在
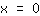
和

都在下降。这说明,当函数导数的符号没有发生变化时,它就不是机制点。这样的 一个点(导数值为
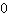
但不是极值点)被叫做鞍点。
如何运用符号改变规则?
- 首先对函数求导。
- 然后求导数的零点。只有零点的 x-值 是极值点的 x-值。
- 然后将导数零点附近的 x-值代入导数中。观察导数值 是否有符号变化。有,则找到了极值点,无,则是鞍点。
为什么说符号改变规则是一个充分条件?
导数为 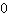 是存在极值点的必要条件(也就是说对于任意极值点都存在导数为 0),但它 并不是充分条件,也就是说,导数为
是存在极值点的必要条件(也就是说对于任意极值点都存在导数为 0),但它 并不是充分条件,也就是说,导数为 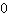 处不一定就是极值点。 (参见上方的鞍点)。
处不一定就是极值点。 (参见上方的鞍点)。
当导数既等于 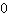 ,又有符号变化, 那么就一定是极值点。在数学中,我们将导数为
,又有符号变化, 那么就一定是极值点。在数学中,我们将导数为 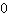 和符号改变叫做存在极值点的 充要条件。
和符号改变叫做存在极值点的 充要条件。
我可以看一些例题吗?
当然,在这里输入你的函数,Mathepower来帮你分步计算函数的极值点。