什么是线性函数(一次函数)?
线性函数是函数图像为一条直线的函数。例如:
你的习题: 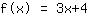
这是方程的图像
|
|
- 零点 在 -1.333
- y-轴截距 在 (0|4)
|
线性函数的图像永远是一条直线。
与线性函数类似的说法也有线性相关。
线性函数的斜率是什么?
线性函数的斜率是变量 x 前的系数。它说明了每当向右走一个单位时,函数向上/向下走的单位量是多少。 例如:
你的习题: 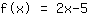
这是方程的图像
|
|
|
函数的斜率为 2。当我们将任意函数上的点 向右移动一小格,函数的图像就要向上移动两小格。
另一个例子,当斜率为负数:
你的习题: 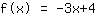
这是方程的图像
|
|
|
这个线性函数的斜率为
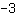
。这表示,当我们向右移动一小格,函数必须要向下 移动三小格。
什么是线性函数的 y-轴截距?
y-轴截距就是函数末尾的数字。像它的名字一样,它表示函数图像于 y-轴的相交点。当我们 看到这两个函数图像,可以知道
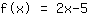
一个函数与 y-轴在
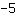
处相切。
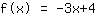
一个函数与 y-轴在
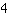
处相切。
如何通过函数的斜率和一个点求线性函数呢?
你需要将点代入方程中,也就是说,一个坐标代入 x,另外一个代入 f(x)。来看这个例题,假设 我们知道函数斜率为 -7,并且通过点 (-2|5)。
你的习题:
点 (-2|5); 斜率 -7;
你的习题: 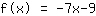
这是方程的图像
|
|
- 零点 在 -1.286
- y-轴截距 在 (0|-9)
Mathepower是这样计算的:
通过代入,计算y-轴截距:
直线方程的一般形式: f(x)=mx+b
代入 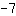 为m, 为m, 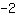 为x,和 为x,和 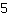 为 f(x)。 为 f(x)。
所以,y轴的截距在 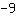
所以,方程等式为: 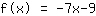
|
要如何通过给出的两个点来计算线性函数方程呢?
首先我们要计算函数的斜率 m。将这两个点的 x轴坐标和 y轴坐标代入公式中:m=(y_2-y_1)/(x_2-x_1)。这说明 通过 y轴坐标的差值除以 x轴坐标的差值,来计算斜率。例如:
你的习题:
点 (1|2); 点 (3|8);
你的习题: 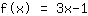
这是方程的图像
|
|
- 零点 在 0.333
- y-轴截距 在 (0|-1)
Mathepower是这样计算的:
计算斜率 m,使用公式: 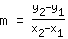
通过代入,计算y-轴截距:
直线方程的一般形式: f(x)=mx+b
代入 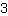 为m, 为m, 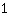 为x,和 为x,和 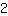 为 f(x)。 为 f(x)。
所以,y轴的截距在 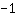
所以,方程等式为: 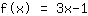
|
可以看到,我们先求出了斜率。再将一个点代入方程中,计算得到 y-轴截距, 从而得到完整的函数方程。
还有其他的例子吗?
当然,只需要输入你自己的习题,Mathepower来帮你一步一步解答。(Mathepower的观点:
你不要仅仅看已经给出的解释,而是要尝试来解释你自己的计算!)