什么是极值点？
函数图像上，极值点是图像在局部达到最高的点（叫做极大值点）或 局部达到最低的点（叫做极小值点）。函数 的最大值或最小值却不一定要在极大、极小值点处。
比如说函数的极值点可能出现在 (0|-3)，但函数的最大值点在 (2|5)。 这表示，最大极值点不一定就是函数的最大值，但一定是局部的最高值， 也就是说在这一点附近，没有比它更高的点。
如何求极值点？
基本思想是在极值点处，点切线的斜率为
。
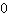
所以求极值点的 基本思路是：
- 找到一个求切线斜率的方法（借助方程求导）。
- 找出在什么时候，切线的斜率为 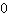。在这就有可能存在极值点（但并不表示必然是一个极值点！）。
这表示：求极值点就是要求导数的零点。
当斜率为 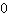时，就必然出现极值点吗？
不。如果斜率为0时，我们可能有一个最大极值点 （见上方），
或斜率为
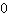
，但并不是极值点。这样的点 叫做鞍点。
在极值点处切线斜率一定为 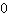吗？
这是正确的。但反过来行不通，正如上述所见。所以得出：切线斜率为
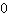
是 存在极值点的必要条件，但并不是充分条件。
当得出切线斜率为 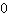后，我们如何判断这个点是最大极值点、最小极值点还是鞍点呢？
使用符号改变规则。
我的家庭作业里有求极值点的习题，但我不会写。我该怎么做呢？
只要在上方输入你的函数！Mathepower来帮你计算，并给出详细解释和解题步骤。