वक्र स्केचिंग का क्या अर्थ है?
वक्र स्केचिंग एक फ़ंक्शन के सभी विशिष्ट बिंदुओं को खोजने के लिए एक गणना है, उदा। जड़ें, y- अक्ष-अवरोधन, अधिकतम और न्यूनतम मोड़, विभक्ति अंक।
उन बिंदुओं को कैसे प्राप्त करें?
डेरिवेटिव की गणना करके। फिर आप फ़ंक्शन के साथ-साथ व्युत्पन्न के बराबर फ़ंक्शन सेट करते हैं शून्य: जड़ समीकरण के समाधान हैं
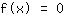
. टर्निंग पॉइंट व्युत्पत्ति की जड़ों में हो सकते हैं, अर्थात्। आप समीकरण हल करेंगे
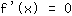
अधिकतम / न्यूनतम मोड़ खोजने के लिए। (यदि नहीं है तो एक मोड़ है व्युत्पत्ति के मूल में, साइन मानदंड के परिवर्तन का उपयोग करके जांच की जा सकती है।) एक विभक्ति बिंदु पर, दूसरी व्युत्पत्ति होनी चाहिए

, इसलिए विभक्ति बिंदुओं को खोजने के लिए समीकरण हल करें
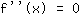
।
आजकल वक्र स्केचिंग कम क्यों की जाती है?
यह थोड़ा बेवकूफी भरा है: आपको बस ऐसा करने का एक तरीका सीखना होगा हर बार उनके अर्थ के बारे में बहुत अधिक सोचने के बिना गणना करें। इसलिए, व्यायाम करें जहां आपको उन बिंदुओं के अर्थ के बारे में सोचना होगा आजकल अधिक महत्वपूर्ण है।
क्या मैं एक उदाहरण देख सकता हूँ?
बेशक। वक्र स्केच करें
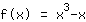
।
mathepower इस कार्य के साथ काम करता है:
यह आपके फ़ंक्शन का ग्राफ़ है।
|
|
- रूट्स पर -1; 0; 1
- y- अक्ष अवरोधन पर (0|0)
- अधिकतम और न्यूनतम मोड़ पर (-0.577|0.385); (0.577|-0.385)
- विभक्ति अंक पर (0|0)
यह Mathepower की गणना है:
मूल:
की जड़ों की तलाश में 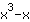
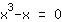 | | | फैक्टर आउट 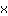 . . |
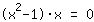 | | | 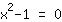 | | | उत्पाद 0. के बराबर है 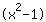 शून्य होना चाहिए…। शून्य होना चाहिए…। |
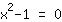 | | | +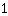 |
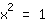 | | | दोनों तरफ चौकोर जड़ लें। |
 | | |  | | | की जड़ निकालें 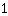 |
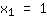 | | |  | | | की जड़ निकालें 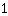 |
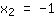 | | | 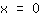 | | | … या कारक  शून्य होना चाहिए शून्य होना चाहिए |
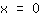 | | |
तो, जड़ें हैं: {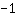 ; ; ; ;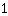 } }
समरूपता:
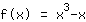 मूल करने के लिए बिंदु सममित है। मूल करने के लिए बिंदु सममित है।
0 डालकर y- अक्ष अवरोधन की गणना करें।
सम्मिलित करें 0 समारोह में 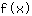 : :
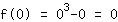
तो, y- अक्ष इंटरसेप्ट पर है (0|0)
समारोह में अंतर करें 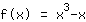
| समारोह में अंतर करें 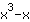 : : | ( की व्युत्पत्ति  ) ) | + | ( की व्युत्पत्ति 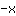 ) ) | 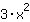 | + | 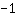 |
तो, के व्युत्पन्न 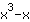 है है 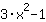 . . |
| |
|
तो पहला व्युत्पन्न है 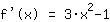
दूसरा व्युत्पन्न, यानी व्युत्पन्न 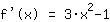 : :
| समारोह में अंतर करें 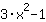 : : | ( की व्युत्पत्ति 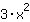 ) ) | + | ( की व्युत्पत्ति 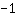 ) ) | 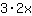 | + |  |
तो, के व्युत्पन्न 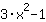 है है 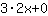 . . |
| |
|
विभेदन को सरल कीजिए:
तो दूसरा व्युत्पन्न है 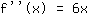
तीसरा व्युत्पन्न, यानी व्युत्पन्न 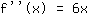 : :
का व्युत्पन्न 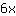 है है 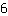
तो तीसरा व्युत्पन्न है 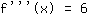
मोड़ की तलाश में।
हमें पहले व्युत्पन्न की जड़ें तलाशनी होगी ।
की जड़ों की तलाश में 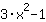
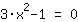 | | | +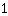 |
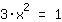 | | | :  |
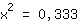 | | | दोनों तरफ चौकोर जड़ लें। |
 | | |  | | | की जड़ निकालें  |
 | | |  | | | की जड़ निकालें  |
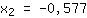 | | |
टर्निंग पॉइंट्स हो सकते हैं {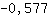 ; ;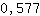 } }
पहली व्युत्पन्न की जड़ों को दूसरी व्युत्पन्न में डालें:
सम्मिलित करें -0.577 समारोह में 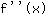 : :
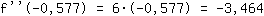
-3.464 0. से कम है इसलिए अधिकतम पर है 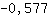 । ।
सम्मिलित करें -0.577 समारोह में 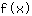 : :
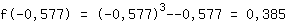
अधिकतम मोड़ (-0.577|0.385)
सम्मिलित करें 0.577 समारोह में 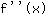 : :

3.464 0. से बड़ा है, इसलिए न्यूनतम पर है 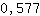 । ।
सम्मिलित करें 0.577 समारोह में 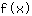 : :
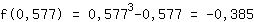
न्यूनतम मोड़ (0.577|-0.385)
विभक्ति अंक की तलाश में।
हमें दूसरे व्युत्पन्न की जड़ें तलाशनी होंगी।
की जड़ों की तलाश में 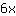
संक्रमण बिंदु पर हो सकता है { } }
तीसरे व्युत्पन्न में दूसरे व्युत्पन्न की जड़ें डालें:
तीसरे व्युत्पन्न में शामिल नहीं है x , इसलिए प्रविष्टि देता है 6
6 0 से बड़ा है, इसलिए इसमें एक विभक्ति बिंदु है  । ।
सम्मिलित करें 0 समारोह में 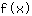 : :
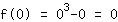
मोड़ बिंदु (0|0)
|