Lcm की गणना करें

दो नंबरों का Lcm उनका सबसे कम सामान्य गुणक है, यानी दोनों संख्याओं द्वारा सबसे छोटा संख्या विभाज्य।

Lcm के लिए क्या आवश्यक है?

उदाहरण के लिए यदि आप एक ही हर पर दो अंश लगाते हैं। उन अंशों का सबसे छोटा संभव भाजक है हर की lcm।

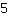
उदाहरण के लिए, और की तुलना करने देता है। सबसे पहले, यह स्पष्ट नहीं है कि कौन सा अंश बड़ा है। परंतु और का lcm है, इसलिए भिन्नों को सामान्य हर पर रखना संभव है:

= और = 6/15।

अब यह आसानी से देखा जा सकता है कि से छोटा है।

lcm - कम से कम सामान्य कई

यह कैलकुलेटर दो संख्याओं का lcm पाता है। बस अपना नंबर दर्ज करें और lcm प्राप्त करें।