रैखिक कार्य क्या है?
एक रैखिक फ़ंक्शन एक फ़ंक्शन है जिसका ग्राफ एक रेखा है। यहाँ एक उदाहरण है:
आपका अभ्यास: 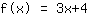
यह आपके फ़ंक्शन का ग्राफ़ है।
|
|
- रूट्स पर -1.333
- y- अक्ष अवरोधन पर (0|4)
|
एक रेखीय फलन का ग्राफ हमेशा एक रेखा होती है।
रेखीय कार्य के लिए एक समान शब्द रैखिक सहसंबंध है।
रैखिक कार्य का ढलान क्या है?
एक रैखिक फ़ंक्शन का ढलान एक्स के सामने की संख्या से मेल खाता है। यह कहता है कि यदि आप एक इकाई को दाईं ओर जाते हैं तो आपको कैसे / नीचे जाना पड़ सकता है। उदाहरण:
आपका अभ्यास: 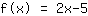
यह आपके फ़ंक्शन का ग्राफ़ है।
|
|
- रूट्स पर 2.5
- y- अक्ष अवरोधन पर (0|-5)
|
हम देखते हैं कि इस कार्य में ढलान है
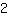
. यदि हम जाते हैं ग्राफ पर किसी भी बिंदु के दाईं ओर एक वर्ग, हमें फिर से ग्राफ पर होने के लिए दो वर्गों पर जाना होगा।
एक और उदाहरण, इस बार नकारात्मक ढलान के साथ:
आपका अभ्यास: 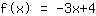
यह आपके फ़ंक्शन का ग्राफ़ है।
|
|
- रूट्स पर 1.333
- y- अक्ष अवरोधन पर (0|4)
|
इस रैखिक कार्य में ढलान
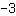
है। इसका मतलब है कि जब भी हम दाईं ओर एक वर्ग में जाते हैं, तो हमें तीन पर जाना पड़ता है वर्गों को फिर से ग्राफ पर होना चाहिए।
एक रेखीय फलन की y- रेखा अवरोधन क्या है?
फ़ंक्शन के अंत में y- लाइन इंटरसेप्ट नंबर है। जैसा कि नाम से पता चलता है, यह कहता है कि फ़ंक्शन कहां y- अक्ष को काटता है। अगर तुम फ़ंक्शन ग्राफ़ पर एक नज़र डालें, आप देखते हैं कि
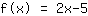
die y-Achse bei
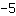
schneidet und
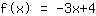
die y-Achse bei
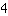
schneidet.
एक बिंदु और ढलान से रेखा के समीकरण की गणना कैसे करें?
आपको बिंदु को समीकरण में सम्मिलित करना होगा, अर्थात् एक x के लिए समन्वय करना और दूसरा f (x) के लिए। यहाँ एक उदाहरण है: मान लेते हैं हम जानते हैं कि हमारे कार्य में ढलान
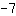
है और
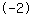
|
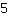
से होकर गुजरता है।
आपका अभ्यास:
बिंदु (-2|5); ढाल -7;
आपका अभ्यास: 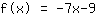
यह आपके फ़ंक्शन का ग्राफ़ है।
|
|
- रूट्स पर -1.286
- y- अक्ष अवरोधन पर (0|-9)
यह Mathepower की गणना है:
सम्मिलित करके y- अक्ष अवरोधन b की गणना करें:
रैखिक समारोह का सामान्य रूप: f(x)=mx+b
सम्मिलित करें 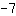 m के लिये, m के लिये, 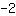 x के लिए और x के लिए और 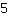 f (x) के लिए। f (x) के लिए।
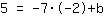 | | | गुणा 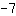 द्वारा द्वारा 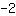 |
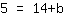 | | | समीकरण के दोनों किनारों को स्वैप करें। |
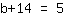 | | | 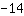 |
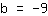 | | |
तो, y- अक्ष इंटरसेप्ट पर है 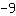
इसलिए, फ़ंक्शन का समीकरण है 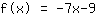
|
दो दिए गए बिंदुओं से एक रैखिक फ़ंक्शन के समीकरण की गणना कैसे करें?
सबसे पहले, हमें x- और y- बिंदुओं के सूत्र m =
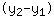
/ /
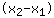
में सम्मिलित करके ढलान m की गणना करनी होगी। इसका मतलब है की: आप y- निर्देशांक के अंतर की गणना करते हैं और इसे x- निर्देशांक के अंतर से विभाजित करते हैं। यहाँ एक उदाहरण है:
आपका अभ्यास:
बिंदु (1|2); बिंदु (3|8);
आपका अभ्यास: 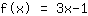
यह आपके फ़ंक्शन का ग्राफ़ है।
|
|
- रूट्स पर 0.333
- y- अक्ष अवरोधन पर (0|-1)
यह Mathepower की गणना है:
ढलान एम की गणना करने के लिए, सूत्र का उपयोग करें 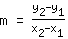 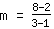 | | | जोड़ना  से से 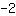 |
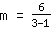 | | | जोड़ना  से से 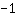 |
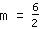 | | | विभाजित 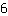 द्वारा द्वारा 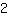 |
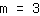 | | |
सम्मिलित करके y- अक्ष अवरोधन b की गणना करें:
रैखिक समारोह का सामान्य रूप: f(x)=mx+b
सम्मिलित करें  m के लिये, m के लिये, 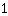 x के लिए और x के लिए और 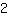 f (x) के लिए। f (x) के लिए।
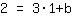 | | |
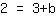 | | | समीकरण के दोनों किनारों को स्वैप करें। |
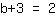 | | | 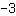 |
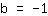 | | |
तो, y- अक्ष इंटरसेप्ट पर है 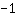
इसलिए, फ़ंक्शन का समीकरण है 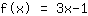
|
जैसा कि हम देख सकते हैं, ढलान की गणना पहले की गई थी। फ़ंक्शन के समीकरण को खोजने के लिए, आपको एक बिंदु सम्मिलित करना होगा और एक अंक प्राप्त करना होगा समीकरण जो y- अक्ष अवरोधन देता है।
क्या मैं और उदाहरण देख सकता हूं?
बेशक। बस ऊपर दिए गए उदाहरणों को दर्ज करें और उन्हें तुरंत चरण-दर-चरण परिकलित किया जाएगा। (यह मैथपावर का विचार है:
आप केवल पहले से ही किए गए कुछ स्पष्टीकरणों को नहीं देखते हैं, लेकिन आप अपनी खुद की गणनाओं को समझाते हैं! ""