यह किसके बारे में है?
यह किसी तरह से वक्र स्केचिंग के विपरीत है। वक्र स्केचिंग का मतलब है कि आपको एक फ़ंक्शन मिला है और देख रहे हैं जड़ों के लिए, मोड़ और विभक्ति अंक। हम यहाँ क्या करते हैं इसके विपरीत है: आपके पास कुछ जड़ें, विभक्ति बिंदु, मोड़ बिंदु आदि हैं और वे होने वाले फ़ंक्शन की तलाश कर रहे हैं।
किसी फ़ंक्शन का पुनर्निर्माण कैसे करें?
मुख्य रूप से, आपको समीकरणों को खोजना होगा और उन्हें हल करना होगा। यह आपको अपने फ़ंक्शन के गुणांक देता है। यहाँ एक उदाहरण है: मान लें कि हम डिग्री

के एक फ़ंक्शन की तलाश कर रहे हैं, जिसमें
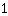
|
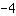
न्यूनतम मोड़ और अधिकतम मोड़
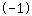

है।
आप के साथ एक समारोह के लिए देख रहे हैं:
द्विघात फंक्शन
अधिकतम मोड़ पर (-1|3)
न्यूनतम मोड़ पर (1|-4)
माथेपॉवर ने निम्न कार्य पाया:
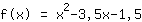
यह आपके फ़ंक्शन का ग्राफ़ है।
|
|
- रूट्स पर -0.386; 3.886
- y- अक्ष अवरोधन पर (0|-1.5)
- अधिकतम और न्यूनतम मोड़ पर (1.75|-4.563)
- विभक्ति अंक
इस प्रकार मैथपॉवर की गणना की जाती है:
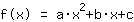
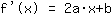
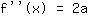
बिंदु पर (-1|3) समीकरण देता है :
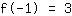
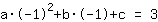
सरलीकृत: :
1a-1b+1c=3
बिंदु पर (1|-4) समीकरण देता है :
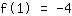
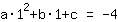
सरलीकृत: :
1a+1b+1c=-4
इसलिए, हमें समीकरणों की निम्नलिखित प्रणाली मिली: :
| a | -1b | +c | = | 3 | | a | +b | +c | = | -4 |
इस तरह से समीकरणों की इस प्रणाली को हल करना है:
| a | -1b | +c | = | 3 | | a | +b | +c | = | -4 |
| | | ( -1 समय रेखा 1 लाइन में जोड़ा गया 2 )
| | ( यह 2 रेखा द्वारा विभाजित किया गया था 2 ) |
| 2 रेखा: | b+0c = -3,5 | | c स्वतंत्र रूप से चुना जा सकता है | | के लिए हल b : : | b = 0c -3,5 |
| 1 रेखा: | | | पहले से ज्ञात चर | | | के लिए हल a : | a = -1c -0,5 |
सेट a के बराबर
इस का मतलब है कि c के बराबर है -1,5
सम्मिलित करने से पता चलता है कि फ़ंक्शन के बराबर है 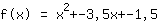 ist. ist.
|
दिए गए बिंदुओं के माध्यम से एक फ़ंक्शन कैसे खोजें?
सामान्य नियम यह है कि किसी भी दिए गए बिंदु के लिए डिग्री
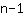
का एक कार्य है जिसका ग्राफ उनके माध्यम से जाता है। तो उदा। आप समीकरणों को हल करके पाते हैं चार बिंदुओं
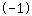
|

के माध्यम से डिग्री

का एक फ़ंक्शन,

|
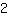
,
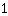
|
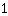
und
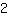
|
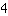
: |
आप के साथ एक समारोह के लिए देख रहे हैं:
डिग्री का कार्य 3
बिंदु पर (-1|3)
बिंदु पर (0|2)
बिंदु पर (1|1)
बिंदु पर (2|4)
माथेपॉवर ने निम्न कार्य पाया:
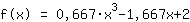
यह आपके फ़ंक्शन का ग्राफ़ है।
|
|
- रूट्स पर -2
- y- अक्ष अवरोधन पर (0|2)
- अधिकतम और न्यूनतम मोड़ पर (-0.913|3.014); (0.913|0.986)
- विभक्ति अंक पर (0|2)
इस प्रकार मैथपॉवर की गणना की जाती है:
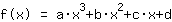
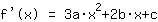
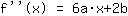
बिंदु पर (-1|3) समीकरण देता है :
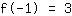
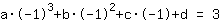
सरलीकृत: :
-1a+1b-1c+1d=3
बिंदु पर (0|2) समीकरण देता है :
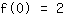
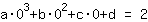
सरलीकृत: :
0a+0b+0c+1d=2
बिंदु पर (1|1) समीकरण देता है :
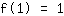
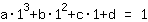
सरलीकृत: :
1a+1b+1c+1d=1
बिंदु पर (2|4) समीकरण देता है :
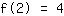
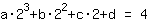
सरलीकृत: :
8a+4b+2c+1d=4
इसलिए, हमें समीकरणों की निम्नलिखित प्रणाली मिली: :
| -1a | +b | -1c | +d | = | 3 | | | | | d | = | 2 | | a | +b | +c | +d | = | 1 | | 8a | +4b | +2c | +d | = | 4 |
इस तरह से समीकरणों की इस प्रणाली को हल करना है:
| -1a | +b | -1c | +d | = | 3 | | | | | d | = | 2 | | a | +b | +c | +d | = | 1 | | 8a | +4b | +2c | +d | = | 4 |
| | | -1a | +b | -1c | +d | = | 3 | | | | | d | = | 2 | | a | +b | +c | +d | = | 1 | | | -4b | -6c | -7d | = | -4 |
| ( -8 समय रेखा 3 लाइन में जोड़ा गया 4 )
| | -1a | +b | -1c | +d | = | 3 | | | | | d | = | 2 | | | 2b | | +2d | = | 4 | | | -4b | -6c | -7d | = | -4 |
| ( 1 समय रेखा 1 लाइन में जोड़ा गया 3 )
| | a | -1b | +c | -1d | = | -3 | | | | | d | = | 2 | | | 2b | | +2d | = | 4 | | | -4b | -6c | -7d | = | -4 |
| ( यह 1 रेखा द्वारा विभाजित किया गया था -1 ) | | a | -1b | +c | -1d | = | -3 | | | | | d | = | 2 | | | 2b | | +2d | = | 4 | | | | -6c | -3d | = | 4 |
| ( 2 समय रेखा 3 लाइन में जोड़ा गया 4 )
| | a | -1b | +c | -1d | = | -3 | | | 2b | | +2d | = | 4 | | | | | d | = | 2 | | | | -6c | -3d | = | 4 |
| ( यह 3 रेखा को आपस में जोड़ा गया था 2 लाइन )
| | a | -1b | +c | -1d | = | -3 | | | b | | +d | = | 2 | | | | | d | = | 2 | | | | -6c | -3d | = | 4 |
| ( यह 2 रेखा द्वारा विभाजित किया गया था 2 ) | | a | -1b | +c | -1d | = | -3 | | | b | | +d | = | 2 | | | | -6c | -3d | = | 4 | | | | | d | = | 2 |
| ( यह 4 रेखा को आपस में जोड़ा गया था 3 लाइन )
| | a | -1b | +c | -1d | = | -3 | | | b | | +d | = | 2 | | | | c | +0,5d | = | -0,667 | | | | | d | = | 2 |
| ( यह 3 रेखा द्वारा विभाजित किया गया था -6 ) |
| 3 रेखा: | | | पहले से ज्ञात चर | | | के लिए हल c : | c = -1,667 |
| 2 रेखा: | | | पहले से ज्ञात चर | | | के लिए हल b : | b = 0 |
| 1 रेखा: | | | पहले से ज्ञात चर | | a | -1⋅0 | +⋅(-1,667) | -1⋅2 | = | -3 |
| | के लिए हल a : | a = 0,667 |
सम्मिलित करने से पता चलता है कि फ़ंक्शन के बराबर है 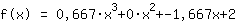 ist. ist.
|
किसी दिए गए विभक्ति बिंदु के साथ एक फ़ंक्शन कैसे खोजें?
एक विभक्ति बिंदु कई समीकरण देता है: एक तरफ, आपको वाई-मान मिला। दूसरी ओर, आप जानते हैं कि ए दूसरी व्युत्पत्ति एक विभक्ति बिंदु पर

है। चलो डिग्री

के एक समारोह के लिए एक उदाहरण पर एक नज़र डालते हैं
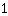
|

में एक विभक्ति बिंदु है।
आप के साथ एक समारोह के लिए देख रहे हैं:
डिग्री का कार्य 3
रूट पर 2
रूट पर 4
मोड़ बिंदु पर (1|3)
माथेपॉवर ने निम्न कार्य पाया:
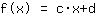
यह आपके फ़ंक्शन का ग्राफ़ है।
|
|
- रूट्स
- y- अक्ष अवरोधन पर (0|0)
- अधिकतम और न्यूनतम मोड़
- विभक्ति अंक
इस प्रकार मैथपॉवर की गणना की जाती है:
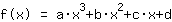
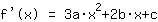
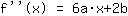
बिंदु पर (1|3) समीकरण देता है :
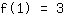
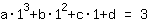
सरलीकृत: :
1a+1b+1c+1d=3
इसलिए, हमें समीकरणों की निम्नलिखित प्रणाली मिली: :
इस तरह से समीकरणों की इस प्रणाली को हल करना है:
| 1 रेखा: | c+1d = 3 | | d स्वतंत्र रूप से चुना जा सकता है | | के लिए हल c : : | c = -1d +3 |
सम्मिलित करने से पता चलता है कि फ़ंक्शन के बराबर है 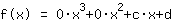 ist. ist.
|
और कैसे मेरे उदाहरण में उपयोग करने के लिए?
बस ऊपर अपने व्यायाम दर्ज करें। मैथपावर दिखाता है कि यह एक निशुल्क चरण-दर-चरण गणना करके कैसे काम करता है। या अभी कोई बना दिलचस्प अभ्यास और जाँच करें कि मैथपावर क्या करता है।