एक मोड़ क्या है?
एक मोड़ एक बिंदु है जहां एक फ़ंक्शन के ग्राफ में स्थानीय रूप से उच्चतम मूल्य (अधिकतम मोड़ कहा जाता है) या है स्थानीय रूप से सबसे कम मूल्य (न्यूनतम मोड़ कहा जाता है)। एक समारोह हालांकि, मोड़ में उनके उच्चतम और निम्नतम मूल्य नहीं हैं।
यह ग्राफ उदा। पर एक अधिकतम मोड़ होता है
|
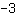
जबकि फ़ंक्शन में उच्च मान होते हैं उदा। में
|
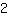
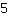
| इसका तात्पर्य है कि एक अधिकतम मोड़, फ़ंक्शन का उच्चतम मूल्य नहीं है, बल्कि स्थानीय रूप से उच्चतम है, यानी उस बिंदु के आसपास एक छोटे से क्षेत्र में कम से कम कोई उच्च मूल्य नहीं है।
टर्निंग पॉइंट कैसे पाएं?
मूल विचार यह है कि एक मोड़ में स्पर्शरेखा में ढलान
है।
तो मूल विचार है टर्निंग पॉइंट्स का पता लगाना है:
- स्पर्शरेखा की ढलानों की गणना करने का एक तरीका खोजें (विभेदन द्वारा संभव)।
- जब स्पर्शरेखा ढलान . है तो खोजें। वहाँ एक मोड़ हो सकता है (लेकिन आवश्यक रूप से एक नहीं है!)
इसका मतलब है: मोड़ को खोजने के लिए, व्युत्पत्ति की जड़ों की तलाश करें।
क्या ढलान का हमेशा मतलब है कि हमारे पास एक महत्वपूर्ण मोड़ है?
यदि ढलान
है, तो हमारे पास अधिकतम मोड़ है (ऊपर दिखाया गया है)
या ढलान सिर्फ एक क्षण के लिए
हो जाता है, हालांकि आपके पास कोई मोड़ नहीं है। ऐसी बात को सैडल पॉइंट कहा जाता है।
क्या मोड़ में ढलान हमेशा होना चाहिए?
हाँ। यह सही है। लेकिन उलटा नहीं, जैसा कि ऊपर देखा गया है। तो हम कहते हैं: ढलान
होना आवश्यक है लेकिन एक मोड़ होने के लिए पर्याप्त नहीं है।
चलो मान लेते हैं कि हमारे पास ढलान है। अगर मेरे पास अधिकतम / न्यूनतम टर्निंग प्वाइंट या काठी बिंदु है तो मैं कैसे पता लगा सकता हूं?
संकेतों की कसौटी के परिवर्तन का उपयोग करके।
मुझे होमवर्क के रूप में टर्निंग पॉइंट तलाशने हैं और पता नहीं कैसे। मैं क्या कर सकता हूँ?
बस अपने फ़ंक्शन को ऊपर दर्ज करें। मैथपॉवर गणना करता है, स्पष्टीकरण और चरण-दर-चरण के साथ।