व्युत्पत्ति क्या है?
X पर किसी फ़ंक्शन की व्युत्पत्ति यह कहती है कि फ़ंक्शन का ग्राफ़ x पर कितना ढलान है, अर्थात्। बिंदु (x | f (x)) में स्पर्शरेखा रेखा क्या है।
उदाहरण: सामान्य परवलय
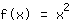
स्पर्शरेखा रेखा
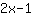
इन
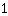
|
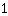
है, अर्थात् ढलान
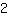
. व्युत्पत्ति सामान्य पैराबोला में x =
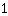
इस प्रकार
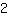
के बराबर है।
व्युत्पत्ति और व्युत्पत्ति समारोह के बीच अंतर क्या है?
व्युत्पत्ति फंक्शन f '(x) ऑफ f (x) एक फंक्शन है जो एक्स को दिए गए एव के लिए एक्स पर ढलान देता है। इसका मतलब है: यह पता लगाने के लिए कि x पर f का ढलान क्या है, आपको बस x को व्युत्पत्ति फ़ंक्शन में दर्ज करना होगा ।
और एक व्युत्पत्ति की गणना कैसे करें?
विभेदन नियमों को खोजने से पहले, किसी को हर बिंदु के लिए अलग-अलग भागफल की गणना करनी होगी। भेदभाव नियमों का उपयोग करके, चीजें सरल हो जाती हैं: सबसे पहले, आप व्युत्पत्ति की गणना करते हैं पॉवर कार्यों की।
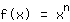
. यह बस है
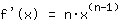
. आगे के नियम व्युत्पत्ति की गणना करना संभव बनाते हैं एक मनमाना बहुपद समारोह, क्योंकि यह सिर्फ शक्ति कार्यों और संख्याओं के उत्पादों का योग है। तो आपको उन नियमों की आवश्यकता है:
- कारक नियम:
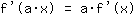
- और योग नियम: की व्युत्पत्ति
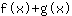 बराबरी
बराबरी 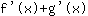
अधिक जटिल कार्यों के लिए, आगे व्युत्पत्ति नियमों की आवश्यकता है:
- उत्पाद नियम: की व्युत्पत्ति
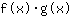 बराबरी
बराबरी 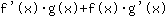
- भागफल नियम: की व्युत्पत्ति
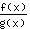 बराबरी
बराबरी 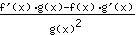
- श्रृंखला नियम: की व्युत्पत्ति
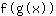 बराबरी
बराबरी 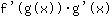
व्युत्पत्ति की रूट्स क्यों खोजें?
व्युत्पत्ति की रूट्स ग्राफ के महत्वपूर्ण बिंदु हैं। अधिकतम या न्यूनतम मोड़ पर, पहली व्युत्पत्ति शून्य के बराबर होती है। (परेशानी की जगह: लेकिन सिर्फ इसलिए कि पहली व्युत्पत्ति शून्य है, एक बिंदु को एक मोड़ नहीं होना चाहिए। आगे की जानकारी के लिए संकेतों के परिवर्तन की जांच करें।) एक विभक्ति बिंदु पर दूसरा व्युत्पन्न शून्य है। तो आप पता लगा सकते हैं व्युत्पत्ति को शून्य के बराबर लगाकर और समीकरण को हल करके अपने कार्य के बारे में बहुत कुछ।