Waar zijn breuken voor nodig?
Een voorbeeld: stel je voor dat
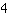
personen een taart willen eten. Hoeveel taart krijgt iedereen? Natuurlijk is de berekening
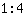
. Maar wat levert het op? Het antwoord is simpelweg om een nieuw getal te maken met de naam
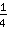
(zeg het: een vierde). Als je het je wilt voorstellen hoeveel dit is, teken gewoon een cake en verdeel deze in vier stukken.
En wat is zo'n breuk?
Wat we zojuist met de taart hebben gedaan, kan met elk natuurlijk getal worden gedaan: stel je voor dat je twee cijfers wilt delen, maar dat komt niet uit. Dan verzin je gewoon een nieuw getal dat het resultaat is van deze deling. Dus de breuk
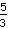
betekent niets anders dan het resultaat van
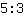
. Het getal bovenaan wordt teller genoemd, het getal onderaan noemer.
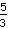
heeft dus teller
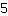
en noemer
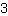
.
En hoe te rekenen met zulke breuken?
Bedenk eerst: er zijn verschillende breuken die hetzelfde getal beschrijven.
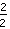
en
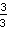
zijn bijvoorbeeld beide hetzelfde als
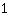
, omdat
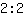
en
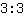
beide
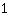
opleveren. Dus we hebben twee breuken die er anders uitzien maar hetzelfde getal beschrijven. Transformeren van een breuk in een andere die hetzelfde getal beschrijft, noemt men uitbreiden of vereenvoudigen.
Als je breuken wilt optellen of aftrekken, moet je ze op dezelfde noemer zetten. Dit kan gedaan worden door het kleinste gemene veelvoud van de noemers te vinden.
Als u breuken wilt vermenigvuldigen, vermenigvuldigt u gewoon de tellers en de noemers. Om breuken te delen, verwissel je de teller en de noemer van de breuk door welke je wilt delen en vervolgens vermenigvuldig je met die breuk.
Hoe noem je de getallen met breuken?
Dat zijn de rationale getallen.