Wat is een extreme waarde?
Een extreme waarde is een punt waar de grafiek van een functie een lokale hoogste waarde heeft (een maximum genoemd) of een lokale laagste waarde (een minimum genoemd). Een functie hoeft echter niet zijn globael hoogste of laagste waarde bij een extreme waarde te hebben.
Deze grafiek b.v. heeft een maximum bij (0|-3) terwijl de functie hogere waarden heeft, b.v. in (2|5). Dit houdt in dat een maximum niet globaal de hoogste waarde van de functie is, maar slechts lokaal de hoogste, d.w.z. er is tenminste geen hogere waarde in een klein gebied rondom dat punt.
Hoe vind je extreme waardeen?
Het basisidee is dat raaklijnen in een extreme waarde helling
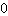
hebben.
Dus het basisidee voor het vinden van extreme waarden is:
- Vind een manier om hellingen van raaklijnen te berekenen (mogelijk door differentiatie).
- Bepaal wanneer de helling van de raaklijn 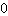is. Er kan een extreme waarde zijn (maar dat is er niet per se!)
Dit betekent: Zoek de nulpunten van de afgeleide om extreme waarden te vinden.
Betekent helling nul altijd dat we een extreme waarde hebben?
Nee. Als de helling
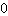
is, dan kan er een maximum (hierboven weergegeven) zijn,
of de helling wordt gewoon even
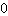
hoewel je geen extreme waarde hebt. Zo'n punt wordt zadelpunt genoemd.
Moet de helling altijd nul zijn bij extreme waarden?
Ja. Als de functie differentierbaar is, is dat juist. Maar het omgekeerde niet, zoals hierboven te zien is. Dus we zeggen: helling
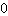
is noodzakelijk maar niet voldoende om een extreme waarde te hebben.
Laten we aannemen dat we helling nul hebben. Hoe kom ik erachter of ik een maximum, minimum of een zadelpunt heb?
Door gebruik te maken van het criterium voor tekenverandering.
Ik moet als huiswerk extreme waarden vinden en weet niet hoe. Wat kan ik doen?
Voer hierboven je functie in. Mathepower doet de berekening, met uitleg en stap voor stap.