Wat betekent functieonderzoek?
Bij een functieonderzoek bepaal je alle karakteristieke punten van een functie, b.v. nulpunten, y-as-snijpunt, maximale en minimale extremen, buigpunten.
Hoe bepaal je die punten?
Door afgeleiden te berekenen. Vervolgens stel je zowel de functie als de afgeleide op nul: Nulpunten zijn oplossingen van de vergelijking
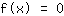
. Extremen kunnen alleen bij de nulpunten van de afgeleide liggen, d.w.z. je moet de vergelijking
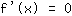
oplossen voor het vinden van extremen. (Of er wel of niet een extreme waarde ligt bij het nulpunt van de afgeleide, kan worden gecontroleerd met behulp van het tekenwijzigingscriterium.) Op een buigpunt moet de tweede afleiding
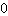
zijn, dus om buigpunten te vinden, lost u de vergelijking
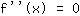
op.
Waarom wordt functieonderzoek tegenwoordig minder gedaan?
Het is nogal zinloos: je berekent domweg naar voorschrift alle mogelijke punten van een functiegrafiek zonder echt na te denken over hun betekenis. Daarom worden tegenwoordig opgaven waar je moet nadenken over de betekenis van die punten belangrijker.
Kan ik een voorbeeld bekijken?
Natuurlijk. Laten we de curve van grafiek
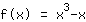
eens bekijken.
Mathepower werkt met deze functie:
Dit is de grafiek van uw functie.
|
|
- Nulpunten bij -1; 0; 1
- y-as snijpunt bij (0|0)
- Minima en maxima bij bij (-0.577|0.385); (0.577|-0.385)
- Buigpunten bij (0|0)
Dit is wat Mathepower heeft berekend:
nulpunten:
Op zoek naar nulpunten van 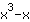
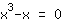 | | | Breng 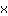 buiten haakjes . buiten haakjes . |
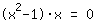 | | | 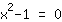 | | | Het product is gelijk aan 0. Dus ofwel de factor 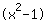 moet nul zijn…. moet nul zijn…. |
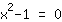 | | | +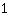 |
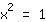 | | | Trek aan beide kanten de vierkantswortel |
 | | |  | | | Trek de wortel van 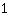 |
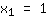 | | |  | | | Trek de wortel van 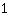 |
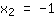 | | | 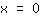 | | | ... of de factor 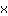 moet nul zijn moet nul zijn |
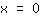 | | |
De nulpunten zijn dus: {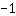 ; ;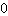 ; ;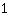 } }
Symmetrie:
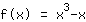 is punt-symmetrisch ten opzichte van de oorsprong. is punt-symmetrisch ten opzichte van de oorsprong.
Bereken het snijpunt van de y-as door 0 in te voegen.
Voer 0 in de functie 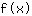 in: in:
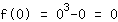
Het snijpunt van de y-as is dus bij (0|0)
Differentieer de functie 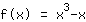
| Differentieer de functie 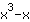 : : | ( Afgeleide van  ) ) | + | ( Afgeleide van 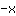 ) ) | 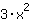 | + | 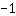 |
Dus de afgeleide van 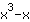 is is 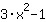 . . |
| |
|
Dus de eerste afgeleide is 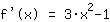
Tweede afgeleide, d.w.z. afgeleide van 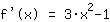 : :
| Differentieer de functie 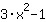 : : | ( Afgeleide van 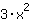 ) ) | + | ( Afgeleide van 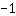 ) ) | 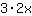 | + | 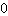 |
Dus de afgeleide van 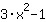 is is 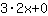 . . |
| |
|
Vereenvoudig de afgeleide:
Dus de tweede afgeleide is 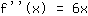
Derde afgeleide, d.w.z. afgeleide van 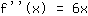 : :
De afgeleide van 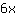 is is 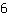
Dus de derde afgeleide is 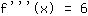
Op zoek naar de extreme waarden
We moeten de nulpunten vinden van de eerste afgeleide.
Op zoek naar nulpunten van 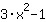
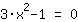 | | | +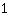 |
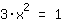 | | | : 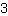 |
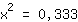 | | | Trek aan beide kanten de vierkantswortel |
 | | |  | | | Trek de wortel van  |
 | | |  | | | Trek de wortel van  |
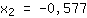 | | |
Extremen zouden kunnen zijn bij {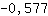 ; ;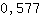 } }
Voeg de nulpunten van de eerste afgeleide in bij de tweede afgeleide:
Voer -0.577 in de functie 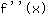 in: in:
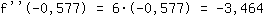
-3.464 is kleiner dan 0. Er is dus een maximum bij 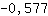 . .
Voer -0.577 in de functie 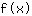 in: in:
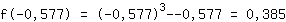
maximum bij (-0.577|0.385)
Voer 0.577 in de functie 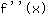 in: in:

3.464 is groter dan 0. Bij 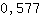 is er dus een minimum. is er dus een minimum.
Voer 0.577 in de functie 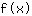 in: in:
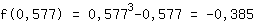
minimum bij (0.577|-0.385)
Op zoek naar buigpunten.
We moeten de nulpunten vinden van de tweede afgeleide.
Op zoek naar nulpunten van 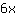
Er kunnen buigpunten zijn bij {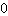 } }
Voeg de nulpunten van de tweede afgeleide in bij de derde afgeleide:
De derde afgeleide bevat geen x , dus invoegen geeft 6
6 is groter dan 0, dus er is bij 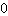 een buigpunt rechts ->links. een buigpunt rechts ->links.
Voer 0 in de functie 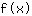 in: in:
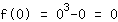
Buigpunt (0|0)
|