Functies vinden


Zoek een functie

Graad van de functie:
1 2 3 4 5

( De graad is de hoogste macht van x die voorkomt. )


Symmetrieën:
as-symmetrisch ten opzichte van de y-as
punt-symmetrisch ten opzichte van de oorsprong


y-as snijpunt



Nulpunten / extremen / buigpunten:
bij x=
bij x=
bij x=
bij x=
bij x=


Karakteristieke punten:
bij |)
bij |)
bij |)
bij (|)
bij (|)


Helling bij gegeven x-coördinaten:
helling bij x=
helling bij x=
helling bij

Wat is functie reconstructie?

Dit is min of meer het tegenovergestelde van functie onderzoek. Functie onderzoek betekent dat je een functie hebt en kijkt naar nulpunten, extreme waarden en buigpunten. Wat we hier doen is het tegenovergestelde: Je hebt sommige nulpunten, buigpunten, toppen enz. en je bent op zoek naar de bijbehorende functie.

Hoe kun je een functie reconstrueren?

In de eerste plaats moet je vergelijkingen zoeken en oplossen. Dit geeft je de coëfficiënten van je functie. Hier is een voorbeeld: Laten we aannemen dat we op zoek zijn naar een 3e graadsfunctie met een dal op (1|-4) en een top op (-1|3).


Je zoekt een functie met:
kwadratische functie
maximum bij bij (-1|3)
minimum bij bij (1|-4)

Mathepower vond de volgende functie:
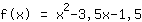
1*f(x)=1*x^2+-3.5*x+-1.5
Dit is de grafiek van uw functie.
Dein Browser unterstützt den HTML-Canvas-Tag nicht. Hol dir einen neuen. :P
  • Nulpunten bij -0.386; 3.886
  • y-as snijpunt bij (0|-1.5)
  • Minima en maxima bij bij (1.75|-4.563)
  • Buigpunten

Dit is hoe Mathepower heeft berekend:
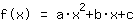
f(x)=1*a*x^2+1*b*x+1*c
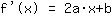
f'(x)=2*a*x+1*b
f''(x)=2*a

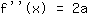
Het punt bij (-1|3) geeft de vergelijking :
f(-1)=3
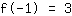
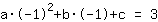
1*a*-1^2+1*b*-1+1*c=3
vereenvoudigd: :
1a-1b+1c=3

Het punt bij (1|-4) geeft de vergelijking :
f(1)=-4
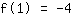
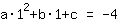
1*a*1^2+1*b*1+1*c=-4
vereenvoudigd: :
1a+1b+1c=-4

Dus we hebben het volgende systeem van vergelijkingen: :
  a   -1b   +c    = 3 
  a   +b   +c    = -4 

Zo lost u dit systeem van vergelijkingen op:
  a   -1b   +c    = 3 
  a   +b   +c    = -4 
  a   -1b   +c    = 3 
     2b       = -7 
 ( -1 keer 1 . regel werd bij de 2 . regel opgeteld. )
  a   -1b   +c    = 3 
     b       = -3,5 
 ( De 2 . regel werd door 2 gedeeld )

2 . regel: b+0c = -3,5
c vrij te kiezen
Voor b oplossen: :   b = 0c -3,5

1 . regel:
a  -1b  +c   =  3
Gebruik reeds bekende variabelen:   
a  -1⋅(0c -3,5)  +⋅1c    =  3
Voor a oplossen: a = -1c -0,5
Stel a gelijk aan 1.
Dit betekent dat c is gelijk aan -1,5

Invoegen laat zien dat de functie gelijk is aan 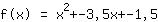f(x)=1*1*x^2+1*-3.5*x+1*-1.5 ist.



Hoe vind ik een functie d.m.v. gegeven punten?

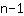
Algemene regel: met n punten is er altijd een functie van graad n-1 die door deze punten gaat. Je vindt dus bijvoorbeeld door het oplossen van vergelijkingen een 3e graadsfunctie door de vier punten (-1|3), (0|2), (1|1) en (2|4):


Je zoekt een functie met:
Functie van graad 3
punt bij (-1|3)
punt bij (0|2)
punt bij (1|1)
punt bij (2|4)

Mathepower vond de volgende functie:
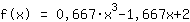
1*f(x)=0.667*x^3+-1.667*x+2
Dit is de grafiek van uw functie.
Dein Browser unterstützt den HTML-Canvas-Tag nicht. Hol dir einen neuen. :P
  • Nulpunten bij -2
  • y-as snijpunt bij (0|2)
  • Minima en maxima bij bij (-0.913|3.014); (0.913|0.986)
  • Buigpunten bij (0|2)

Dit is hoe Mathepower heeft berekend:
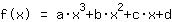
f(x)=1*a*x^3+1*b*x^2+1*c*x+1*d
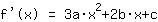
f'(x)=3*a*x^2+2*b*x+1*c
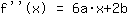
f''(x)=6*a*x+2*b

Het punt bij (-1|3) geeft de vergelijking :
f(-1)=3
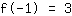
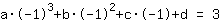
1*a*-1^3+1*b*-1^2+1*c*-1+1*d=3
vereenvoudigd: :
-1a+1b-1c+1d=3

Het punt bij (0|2) geeft de vergelijking :
f(0)=2
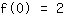
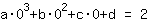
1*a*0^3+1*b*0^2+1*c*0+1*d=2
vereenvoudigd: :
0a+0b+0c+1d=2

Het punt bij (1|1) geeft de vergelijking :
f(1)=1
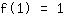
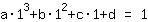
1*a*1^3+1*b*1^2+1*c*1+1*d=1
vereenvoudigd: :
1a+1b+1c+1d=1

Het punt bij (2|4) geeft de vergelijking :
f(2)=4
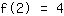
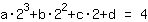
1*a*2^3+1*b*2^2+1*c*2+1*d=4
vereenvoudigd: :
8a+4b+2c+1d=4

Dus we hebben het volgende systeem van vergelijkingen: :
  -1a   +b   -1c   +d    = 3 
           d    = 2 
  a   +b   +c   +d    = 1 
  8a   +4b   +2c   +d    = 4 

Zo lost u dit systeem van vergelijkingen op:
  -1a   +b   -1c   +d    = 3 
           d    = 2 
  a   +b   +c   +d    = 1 
  8a   +4b   +2c   +d    = 4 
  -1a   +b   -1c   +d    = 3 
           d    = 2 
  a   +b   +c   +d    = 1 
     -4b   -6c   -7d    = -4 
 ( -8 keer 3 . regel werd bij de 4 . regel opgeteld. )
  -1a   +b   -1c   +d    = 3 
           d    = 2 
     2b      +2d    = 4 
     -4b   -6c   -7d    = -4 
 ( 1 keer 1 . regel werd bij de 3 . regel opgeteld. )
  a   -1b   +c   -1d    = -3 
           d    = 2 
     2b      +2d    = 4 
     -4b   -6c   -7d    = -4 
 ( De 1 . regel werd door -1 gedeeld )
  a   -1b   +c   -1d    = -3 
           d    = 2 
     2b      +2d    = 4 
        -6c   -3d    = 4 
 ( 2 keer 3 . regel werd bij de 4 . regel opgeteld. )
  a   -1b   +c   -1d    = -3 
     2b      +2d    = 4 
           d    = 2 
        -6c   -3d    = 4 
 ( de 3 regel werd met de 2 regel verwisseld )
  a   -1b   +c   -1d    = -3 
     b      +d    = 2 
           d    = 2 
        -6c   -3d    = 4 
 ( De 2 . regel werd door 2 gedeeld )
  a   -1b   +c   -1d    = -3 
     b      +d    = 2 
        -6c   -3d    = 4 
           d    = 2 
 ( de 4 regel werd met de 3 regel verwisseld )
  a   -1b   +c   -1d    = -3 
     b      +d    = 2 
        c   +0,5d    = -0,667 
           d    = 2 
 ( De 3 . regel werd door -6 gedeeld )


4 . regel:
      d   =  2

3 . regel:
    c  +0,5d   =  -0,667
Gebruik reeds bekende variabelen:   
    c  +0,5⋅2   =  -0,667
Voor c oplossen: c = -1,667

2 . regel:
  b    +d   =  2
Gebruik reeds bekende variabelen:   
  b    +⋅2   =  2
Voor b oplossen: b = 0

1 . regel:
a  -1b  +c  -1d   =  -3
Gebruik reeds bekende variabelen:   
a  -1⋅0  +⋅(-1,667)  -1⋅2   =  -3
Voor a oplossen: a = 0,667

Invoegen laat zien dat de functie gelijk is aan 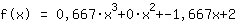f(x)=1*0.667*x^3+1*0*x^2+1*-1.667*x+1*2 ist.



Hoe vind ik een functie met een gegeven buigpunt?

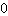
Een buigpunt geeft meerdere vergelijkingen: enerzijds heb je de y-waarde. Aan de andere kant weet je dat de tweede afgeleide gelijk is aan 0 op een buigpunt. Laten we een voorbeeld bekijken voor een 3e graadsfunctie met een buigpunt op (1|3):


Je zoekt een functie met:
Functie van graad 3
nulpunt bij 2
nulpunt bij 4
Buigpunt bij (1|3)

Mathepower vond de volgende functie:
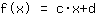
1*f(x)=1*c*x+1*d
Dit is de grafiek van uw functie.
Dein Browser unterstützt den HTML-Canvas-Tag nicht. Hol dir einen neuen. :P
  • Nulpunten
  • y-as snijpunt bij (0|0)
  • Minima en maxima bij
  • Buigpunten

Dit is hoe Mathepower heeft berekend:
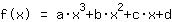
f(x)=1*a*x^3+1*b*x^2+1*c*x+1*d
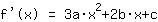
f'(x)=3*a*x^2+2*b*x+1*c
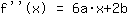
f''(x)=6*a*x+2*b

Het punt bij (1|3) geeft de vergelijking :
f(1)=3
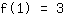
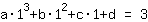
1*a*1^3+1*b*1^2+1*c*1+1*d=3
vereenvoudigd: :
1a+1b+1c+1d=3

Dus we hebben het volgende systeem van vergelijkingen: :
  a   +b   +c   +d    = 3 

Zo lost u dit systeem van vergelijkingen op:
  a   +b   +c   +d    = 3 

1 . regel: c+1d = 3
d vrij te kiezen
Voor c oplossen: :   c = -1d +3

Invoegen laat zien dat de functie gelijk is aan 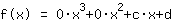f(x)=1*0*x^3+1*0*x^2+1*c*x+1*d ist.



En hoe pas ik dat toe in mijn voorbeeld?

Voer hierboven jouw opgave in. Mathepower laat zien hoe het werkt door een gratis stapsgewijze berekening uit te voeren. Of verzin er gewoon een interessante oefening en bekijk wat Mathepower doet.