تغير الإشارة

ما فائدة تغير الإشارة؟

تحتوي هذه الدالة على ميل في (2|1) ونقطة عظمى. عند x = يصعد الرسم البياني ، أي أن المشتق أكبر من هنا. عند x = ينخفض ​​الرسم البياني ، أي أن المشتق أقل من . وهذا يعني أنه عند نقطة عظمى ، فإن إشارة المشتق هو + قبل و- بعد نقطة التحول. هذا يعني أن إشارات التغيرات المشتقة من + إلى -.

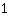
تحتوي هذه الدالة على ميل في | ، ولكن بحد صغرى نقطة تحول. عند x = يقع الرسم البياني ، أي أن الإشتقاق هنا أقل من . عند x = يصعد الرسم البياني ، أي أن الإشتقاق أكبر من . وهذا يعني أنه عند نقطة تحول كحد صغرى ، إشارة الإشتقاق - قبل و + بعد نقطة التحول. هذا يعني إشارات الإشتقاق التغيرات من - إلى +.

تحتوي هذه الدالة أيضًا على ميل عند (2|1) ، ولكن لا توجد نقطة تحول. ترى أن الرسم البياني يصعد عند x = وكذلك عند x = . هذا يعني أنه ليس لديك نقطة تحول إذا كان الإشتقاق لا يغير الإشارات. هذه النقطة (التي ليست نقطة تحول ولكن لها إشتقاق تسمى نقطة انعدام الميل.

كيفية استخدام معيار تغير الإشارة؟

• قم أولاً بإشتقاق الدلة.
• ثم احسب جذور الإشتقاق. فقط تلك الجذور يمكن أن تكون إحداثيات x لنقاط التحول.
• ثم تقوم بتعويض x بقيم قريبة من الصفر في الإشتقاق. إذا كان الإشتقاق يغير الإشارات حول الصفر ، فقد وجدت نقطة تحول. وإلا لا.

لماذا معيار تغير الإشارة كافٍ؟

الإشتقاق كونه ضروريًا لنقطة تحول (أي أنه دائمًا ما يكون عند نقطة تحول). لكن ذلك ليس ضروريًا ، ما يعني ، فقط لأن الإشتقاق هو ، لا يجب أن تكون هناك نقطة تحول (تحقق من نقطة انعدام الميل أعلاه).
إذا كان الإشتقاق ليس فقط ، ولكن أيضًا يغير الإشارات ، فيجب أن يكون لديك نقطة تحول. في الرياضيات ، نقول أن الإشتقاق وتغير الإشارات كافٍ للحصول على نقطة تحول.

هل يمكنني رؤية مثال؟

بالطبع. هذا هو Mathepower. فقط أدخل دالة واحصل على نقاط التحول المحسوبة خطوة بخطوة.