ما هو المشتق؟
يشير إشتقاق دالة عند النقطة x إلى ميل الرسم البياني للدالة عند النقطة x ، أي ميل المماس للرسم البياني عند النقطة (x | f (x)).
مثال: القطع المكافئ العادي
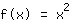
له المماس
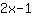
عند النقطة
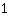
|
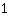
، أي الميل

. وبالتالي فإن مشتق القطع المكافئ العادي عند x =
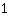
يساوي

.
ما الفرق بين الإشتقاق ودالة الإشتقاق؟
دالة الإشتقاق f '(x) من f (x) هي دالة تعطي الميل عند x لكل x معين. هذا يعني: لمعرفة ما هو ميل f عند x ، عليك فقط إدخال x في دالة الإشتقاق بالعامية ، غالبًا ما يقول المرء الإشتقاق بدلاً من دالة الإشتقاق.
وكيف تحسب الإشتقاق؟
قبل أن تكتشف قواعد الإشتقاق ، يجب عليك استخدام حاصل الفرق لحساب كل نقطة مشتقة لها وظيفة هناك. يتم تسهيل ذلك بمساعدة قواعد الإشتقاق: أولاً ، يتم تحديد مشتق الدوال الأسية
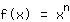
. ببساطة
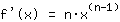
. يمكن استخدام قواعد أخرى لحساب إشتقاق أي دالة منطقية تمامًا ، والتي هي ببساطة مجموع منتجات الدوال الأسية مع الأرقام. لذلك أنت بحاجة إلى هذه القواعد
- قاعدة العامل الثابت
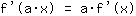
- وقاعدة المجموع: إشتقاق الدالة
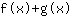 يساوي
يساوي 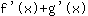
للحصول على وظائف أكثر تعقيدًا ، هناك المزيد من قواعد الإشتقاق المطلوبة:
- قاعدة الضرب: إشتقاق الدالة
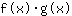 يساوي
يساوي 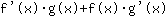
- قاعدة ناتج القسمة: إشتقاق التابع
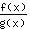 يساوي
يساوي 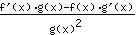
- قاعدة السلسلة: إشتقاق الدالة
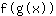 يساوي
يساوي 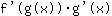
لماذا علينا أن نحدد جذور الإشتقاق ؟
عادةً ما تكون الأصفار للمشتق نقاطًا مهمة في الرسم البياني للدالة. في نقطة قصوى أو دنيا ، المشتق الأول هو صفر. (.تنبيه ، لا ينطبق العكس: فقط لأن المشتق يساوي صفر ، لا يجب أن تكون النقطة نقطة عالية أو منخفضة ، انظر معيار تغيير الإشارة) عند نقطة التحول ، يكون المشتق الثاني صفرًا. إِذَنْ يمكنك معرفة الكثير عن الدالة الخاصة بك عن طريق وضع الإشتقاق يساوي الصفر وحل المعادلة.