الكسور

لماذا نحتاج الى الكسور؟

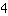
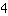
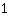
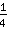
المثال الأول: تخيل أشخاص يريدون أكل كعكة. ما مقدار الكعكة التي يحصل عليها كل شخص؟ بالطبع، الحساب هو : . لكن ما هي النتيجة؟ الجواب ببساطة هو إنشاء رقم جديد يسمى (يقال له: ربع). إذا كنت تريد أن تتخيل كم هذا ، ارسم كعكة فقط واقطعها إلى أربع قطع.

ما هو اذا الكسر؟

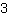
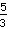
ما فعلناه للتو مع الكعكة ، يمكن القيام به مع كل رقم: تخيل أنك تريد تقسيم رقمين ، لكن هذا غير ممكن. ثم، إنك تريد تشكل رقمًا جديدًا يكون نتيجة هذا التقسيم. لذا فإن الكسر%5%3% لا يعني أي شيء آخر غير النتيجة : . الرقم أعلاه يسمى البسط ، والرقم السفلي يسمى المقام . إذاً له البسط والمقام .

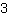
وكيف تحسب هذه الكسور؟

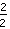
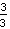
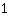
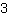
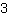
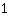
ضع في اعتبارك أولاً: هناك كسور مختلفة المظهر تصف نفس الرقم. على سبيل المثال ، و كلاهما مثل ، السبب : و : كلاهما يعطي . لذا لدينا جزئين مختلفين ولكن يصفان نفس العدد. تحويل الكسر إلى آخر يصف نفس الرقم يسمى توسيع أو اختزال الكسر.

إذا كنت ترغب في إضافة أو طرح الكسور ، فيجب عليك وضعها على نفس المقام. يمكن القيام بذلك من خلال إيجاد المضاعف المشترك الأصغر من القواسم.

إذا كنت ترغب في ضرب الكسور ، فقط اضرب البسط والمقام. لتقسيم الكسور بدّل البسط ومقام الكسر الذي تريد القسمة عليه ، ثم اضرب تلك الكسور

ما اسم نطاق الأرقام التي تنتمي إليها الكسور (أكبر أو أقل من الصفر)؟

هذه هي الأعداد الكسرية.