Ableiten

<


Gib hier die Funktion ein, die abgeleitet werden soll.
Eingabetipps: Gib als 3*x^2 ein,
als (x+1)/(x-2x^4) und
als 3/5.

Was ist die Ableitung?

Die Ableitung einer Funktion an der Stelle x gibt an, welche Steigung der Graph der Funktion an der Stelle x hat, das heißt, welche Steigung eine Tangente an den Graphen im Punkt (x|f(x)) hat.

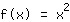
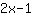
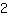
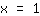
Beispiel: Die Normalparabel f_f(x)=x^2 hat im Punkt (1|1) die Tangente 2x-1, also die Steigung 2. Die Ableitung der Normalparabel bei x=1 ist also gleich 2.

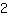
Was ist der Unterschied zwischen der Ableitung und der Ableitungsfunktion?

Die Ableitungsfunktion f'(x) einer Funktion f(x) ist eine Funktion, die für jeden Wert x die Ableitung von x angibt. Soll heißen: Um die Steigung des Graphen von f an der Stelle x zu bestimmen, muss man einfach nur x in die Ableitungsfunktion einsetzen. Umgangssprachlich sagt man statt Ableitungsfunktion aber häufig auch einfach Ableitung.

Und wie berechnet man eine Ableitung?

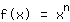
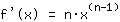
Bevor man die Ableitungsregeln entdeckt hat, muss man mit Hilfe des Differenzenquotienten für jeden Punkt einzeln ausrechnen, welche Ableitung die Funktion dort hat. Mit Hilfe der Ableitungsregeln wird dies einfacher: Zunächst bestimmt man die Ableitung von Potenzfunktionen f_f(x)=x^n. Diese lautet nämlich einfach f_f'(x)=nx^(n-1). Mit weiteren Regeln kann man die Ableitung einer beliebigen ganzrationalen Funktion ausrechnen, die ja einfach nur Summe von Produkten von Potenzfunktionen mit Zahlen ist. Dafür braucht man nur
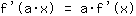
  • die Faktorregel: f_f'(a*x)=a*f_f'(x)
  • und die Summenregel: Die Ableitung der Funktion 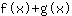ist gleich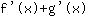
Für kompliziertere Funktionen braucht man weitere Ableitungsregeln wie
  • die Produktregel: Die Abletiung der Funktion 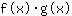ist gleich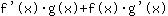
  • die Quotientenregel: Die Ableitung der Funktion 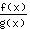ist gleich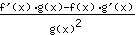
  • die Kettenregel: Die Ableitung der Funktion 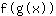ist gleich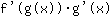

Wozu bestimmt man die Nullstellen einer Ableitung?

Die Nullstellen einer Ableitung sind meist wichtige Punkte des Funktionsgraphen. An einem Hoch- oder Tiefpunkt ist die erste Ableitung gleich Null. (Vorsicht, die Umkehrung gilt nicht: Nur weil die Ableitung Null ist, muss ein Punkt kein Hoch- oder Tiefpunkt sein, siehe Vorzeichenwechselkriterium. ) An einem Wendepunkt ist die zweite Ableitung gleich Null. Also erfährt man viel über eine Funktion, wenn man die Ableitungen der Funktion gleich Null setzt und die entsprechende Gleichung löst.