Rekonstruktion von Funktionen Rechner

Einfach Aufgabe eingeben und lösen lassen


Funktion gesucht

Grad der Funktion:
1 2 3 4 5

(Der Grad ist der höchste Exponent hinter einem x.)


Symmetrien:
achsensymmetrisch zur y-Achse
punktsymmetrisch zum Ursprung


y-Achsenabschnitt:



Null-/Extrem-/Wendestellen:
bei x=
bei x=
bei x=
bei x=
bei x=


Besondere Punkte:
bei (|)
bei (|)
bei (|)
bei (|)
bei (|)


Steigungen an Stellen:
Steigung bei x=
Steigung bei x=
Steigung bei x=

Was sind Steckbriefaufgaben?

Steckbriefaufgaben sind das Gegenstück zur Kurvendiskussion. Bei einer Kurvendiskussion hat man eine Funktion gegeben und möchte ihre Nullstellen, Hoch-, Tief- und Wendepunkte berechnen. Bei einer Steckbriefaufgabe (auch bekannt als Rekonstruktionsaufgabe / Rekonstruktion von Funktionen) hat man einige Punkte gegeben und sucht eine Funktion, die durch diese Punkte verläuft.

Wie rekonstruiert man eine Funktion?

Dazu muss man vor allem Gleichungen aufstellen und lösen und erhält daraus die Koeffizienten der Funktion. Hier ein Beispiel: Angenommen, man sucht eine Funktion vom Grad 3, die bei (1|-4) einen Tiefpunkt hat sowie bei (-1|3) einen Hochpunkt.


Du suchst eine Funktion mit folgenden Eigenschaften:
quadratische Funktion
Hochpunkt bei (-1|3)
Tiefpunkt bei (1|-4)

Mathepower denkt, dass deine Aufgabe nicht lösbar ist.

Mathepower fand folgende Funktion:
1*f(x)=1.75*x^3+-5.25*x+-0.5
Hier siehst du den Graphen deiner Funktion.
Dein Browser unterstützt den HTML-Canvas-Tag nicht. Hol dir einen neuen. :P
  • Nullstellen bei -1.682; -0.096; 1.778
  • y-Achsenabschnitt bei (0|-0.5)
  • Hochpunkte, Tiefpunkte bei (-1|3); (1|-4)
  • Wendepunkte bei (0|-0.5)

So hat Mathepower gerechnet:
Mit dem von dir gewünschten Grad gibt es keine solche Funktion. Aber es gibt eine von Grad 3.
f(x)=1*a*x^3+1*b*x^2+1*c*x+1*d
f'(x)=3*a*x^2+2*b*x+1*c
f''(x)=6*a*x+2*b

Punkt (-1|3) liefert Gleichung:
f(-1)=3
1*a*-1^3+1*b*-1^2+1*c*-1+1*d=3
vereinfacht:
-1a+1b-1c+1d=3

Hochpunkt (-1|3) liefert Gleichung:
f'(-1)=0
3*a*-1^2+2*b*-1+1*c=0
vereinfacht:
3a-2b+1c+0d=0

Punkt (1|-4) liefert Gleichung:
f(1)=-4
1*a*1^3+1*b*1^2+1*c*1+1*d=-4
vereinfacht:
1a+1b+1c+1d=-4

Tiefpunkt (1|-4) liefert Gleichung:
f'(1)=0
3*a*1^2+2*b*1+1*c=0
vereinfacht:
3a+2b+1c+0d=0

Insgesamt erhält man folgendes Gleichungssystem:
  -1a   +b   -1c   +d    = 3 
  3a   -2b   +c       = 0 
  a   +b   +c   +d    = -4 
  3a   +2b   +c       = 0 

So formt man das Gleichungssystem um:
  -1a   +b   -1c   +d    = 3 
  3a   -2b   +c       = 0 
  a   +b   +c   +d    = -4 
  3a   +2b   +c       = 0 
  -1a   +b   -1c   +d    = 3 
  3a   -2b   +c       = 0 
  a   +b   +c   +d    = -4 
     -1b   -2c   -3d    = 12 
 ( das -3-fache der dritten Zeile wurde zur vierten Zeile addiert )
  -1a   +b   -1c   +d    = 3 
  3a   -2b   +c       = 0 
     1,667b   +0,667c   +d    = -4 
     -1b   -2c   -3d    = 12 
 ( das -0,333-fache der zweiten Zeile wurde zur dritten Zeile addiert )
  -1a   +b   -1c   +d    = 3 
     b   -2c   +3d    = 9 
     1,667b   +0,667c   +d    = -4 
     -1b   -2c   -3d    = 12 
 ( das 3-fache der ersten Zeile wurde zur zweiten Zeile addiert )
  a   -1b   +c   -1d    = -3 
     b   -2c   +3d    = 9 
     1,667b   +0,667c   +d    = -4 
     -1b   -2c   -3d    = 12 
 ( die erste Zeile wurde durch -1 geteilt )
  a   -1b   +c   -1d    = -3 
     b   -2c   +3d    = 9 
     1,667b   +0,667c   +d    = -4 
        -1,6c   -2,4d    = 9,6 
 ( das 0,6-fache der dritten Zeile wurde zur vierten Zeile addiert )
  a   -1b   +c   -1d    = -3 
     b   -2c   +3d    = 9 
        4c   -4d    = -19 
        -1,6c   -2,4d    = 9,6 
 ( das -1,667-fache der zweiten Zeile wurde zur dritten Zeile addiert )
  a   -1b   +c   -1d    = -3 
     b   -2c   +3d    = 9 
        4c   -4d    = -19 
           -4d    = 2 
 ( das 0,4-fache der dritten Zeile wurde zur vierten Zeile addiert )
  a   -1b   +c   -1d    = -3 
     b   -2c   +3d    = 9 
        c   -1d    = -4,75 
           -4d    = 2 
 ( die dritte Zeile wurde durch 4 geteilt )
  a   -1b   +c   -1d    = -3 
     b   -2c   +3d    = 9 
        c   -1d    = -4,75 
           d    = -0,5 
 ( die vierte Zeile wurde durch -4 geteilt )


vierte Zeile:
      d   =  -0,5

dritte Zeile:
    c  -1d   =  -4,75
Schon berechnete Variablen einsetzen:  
    c  -1⋅(-0,5)   =  -4,75
Nach c freistellen: c = -5,25

zweite Zeile:
  b  -2c  +3d   =  9
Schon berechnete Variablen einsetzen:  
  b  -2⋅(-5,25)  +3⋅(-0,5)   =  9
Nach b freistellen: b = 0

erste Zeile:
a  -1b  +c  -1d   =  -3
Schon berechnete Variablen einsetzen:  
a  -1⋅0  +⋅(-5,25)  -1⋅(-0,5)   =  -3
Nach a freistellen: a = 1,75

Einsetzen liefert also, dass die Funktion gleich f(x)=1*1.75*x^3+1*0*x^2+1*-5.25*x+1*-0.5 ist.



Wie findet man eine Funktion durch gegebene Punkte?

Allgemeine Regel: Durch n Punkte gibt es immer eine Funktion vom Grad n-1. Also findet man zum Beispiel durch Gleichunglösen eine Funktion vom Grad 3 durch die vier Punkte (-1|3), (0|2), (1|1) und (2|4):


Du suchst eine Funktion mit folgenden Eigenschaften:
Funktion vom Grad 3
Punkt bei (-1|3)
Punkt bei (0|2)
Punkt bei (1|1)
Punkt bei (2|4)

Mathepower fand folgende Funktion:
1*f(x)=0.667*x^3+-1.667*x+2
Hier siehst du den Graphen deiner Funktion.
Dein Browser unterstützt den HTML-Canvas-Tag nicht. Hol dir einen neuen. :P
  • Nullstellen bei -2
  • y-Achsenabschnitt bei (0|2)
  • Hochpunkte, Tiefpunkte bei (-0.913|3.014); (0.913|0.986)
  • Wendepunkte bei (0|2)

So hat Mathepower gerechnet:
f(x)=1*a*x^3+1*b*x^2+1*c*x+1*d
f'(x)=3*a*x^2+2*b*x+1*c
f''(x)=6*a*x+2*b

Punkt (-1|3) liefert Gleichung:
f(-1)=3
1*a*-1^3+1*b*-1^2+1*c*-1+1*d=3
vereinfacht:
-1a+1b-1c+1d=3

Punkt (0|2) liefert Gleichung:
f(0)=2
1*a*0^3+1*b*0^2+1*c*0+1*d=2
vereinfacht:
0a+0b+0c+1d=2

Punkt (1|1) liefert Gleichung:
f(1)=1
1*a*1^3+1*b*1^2+1*c*1+1*d=1
vereinfacht:
1a+1b+1c+1d=1

Punkt (2|4) liefert Gleichung:
f(2)=4
1*a*2^3+1*b*2^2+1*c*2+1*d=4
vereinfacht:
8a+4b+2c+1d=4

Insgesamt erhält man folgendes Gleichungssystem:
  -1a   +b   -1c   +d    = 3 
           d    = 2 
  a   +b   +c   +d    = 1 
  8a   +4b   +2c   +d    = 4 

So formt man das Gleichungssystem um:
  -1a   +b   -1c   +d    = 3 
           d    = 2 
  a   +b   +c   +d    = 1 
  8a   +4b   +2c   +d    = 4 
  -1a   +b   -1c   +d    = 3 
           d    = 2 
  a   +b   +c   +d    = 1 
     -4b   -6c   -7d    = -4 
 ( das -8-fache der dritten Zeile wurde zur vierten Zeile addiert )
  -1a   +b   -1c   +d    = 3 
           d    = 2 
     2b      +2d    = 4 
     -4b   -6c   -7d    = -4 
 ( das 1-fache der ersten Zeile wurde zur dritten Zeile addiert )
  a   -1b   +c   -1d    = -3 
           d    = 2 
     2b      +2d    = 4 
     -4b   -6c   -7d    = -4 
 ( die erste Zeile wurde durch -1 geteilt )
  a   -1b   +c   -1d    = -3 
           d    = 2 
     2b      +2d    = 4 
        -6c   -3d    = 4 
 ( das 2-fache der dritten Zeile wurde zur vierten Zeile addiert )
  a   -1b   +c   -1d    = -3 
     2b      +2d    = 4 
           d    = 2 
        -6c   -3d    = 4 
 ( die dritte Zeile wurde mit der zweiten Zeile vertauscht )
  a   -1b   +c   -1d    = -3 
     b      +d    = 2 
           d    = 2 
        -6c   -3d    = 4 
 ( die zweite Zeile wurde durch 2 geteilt )
  a   -1b   +c   -1d    = -3 
     b      +d    = 2 
        -6c   -3d    = 4 
           d    = 2 
 ( die vierte Zeile wurde mit der dritten Zeile vertauscht )
  a   -1b   +c   -1d    = -3 
     b      +d    = 2 
        c   +0,5d    = -0,667 
           d    = 2 
 ( die dritte Zeile wurde durch -6 geteilt )


vierte Zeile:
      d   =  2

dritte Zeile:
    c  +0,5d   =  -0,667
Schon berechnete Variablen einsetzen:  
    c  +0,5⋅2   =  -0,667
Nach c freistellen: c = -1,667

zweite Zeile:
  b    +d   =  2
Schon berechnete Variablen einsetzen:  
  b    +⋅2   =  2
Nach b freistellen: b = 0

erste Zeile:
a  -1b  +c  -1d   =  -3
Schon berechnete Variablen einsetzen:  
a  -1⋅0  +⋅(-1,667)  -1⋅2   =  -3
Nach a freistellen: a = 0,667

Einsetzen liefert also, dass die Funktion gleich f(x)=1*0.667*x^3+1*0*x^2+1*-1.667*x+1*2 ist.



Wie findet man eine Funktion zu einem gegebenen Wendepunkt?

Ein Wendepunkt liefert ja mehrere Gleichungen: Zum einen weiß man seine y-Koordinate, zum anderen weiß man, dass dort die zweite Ableitung 0 ist. Hier sehen wir ein Beispiel für eine Funktion von Grad 3, die bei (1|3) einen Wendepunkt hat:


Du suchst eine Funktion mit folgenden Eigenschaften:
Funktion vom Grad 3
Nullstelle bei 2
Nullstelle bei 4
Wendepunkt bei (1|3)

Mathepower fand folgende Funktion:
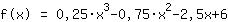
1*f(x)=0.25*x^3+-0.75*x^2+-2.5*x+6
Hier siehst du den Graphen deiner Funktion.
Dein Browser unterstützt den HTML-Canvas-Tag nicht. Hol dir einen neuen. :P
  • Nullstellen bei -3; 2; 4
  • y-Achsenabschnitt bei (0|6)
  • Hochpunkte, Tiefpunkte bei (-1.082|7.51); (3.082|-1.51)
  • Wendepunkte bei (1|3)

So hat Mathepower gerechnet:
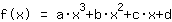
f(x)=1*a*x^3+1*b*x^2+1*c*x+1*d
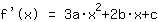
f'(x)=3*a*x^2+2*b*x+1*c
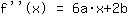
f''(x)=6*a*x+2*b

Nullstelle bei 2 liefert Gleichung:
f(2)=0
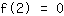
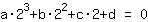
1*a*2^3+1*b*2^2+1*c*2+1*d=0
vereinfacht:
8a+4b+2c+1d=0

Nullstelle bei 4 liefert Gleichung:
f(4)=0
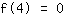
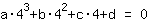
1*a*4^3+1*b*4^2+1*c*4+1*d=0
vereinfacht:
64a+16b+4c+1d=0

Punkt (1|3) liefert Gleichung:
f(1)=3
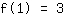
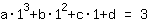
1*a*1^3+1*b*1^2+1*c*1+1*d=3
vereinfacht:
1a+1b+1c+1d=3

Wendepunkt (1|3) liefert Gleichung:
f''(1)=0
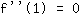
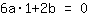
6*a*1+2*b=0
vereinfacht:
6a+2b+0c+0d=0

Insgesamt erhält man folgendes Gleichungssystem:
  8a   +4b   +2c   +d    = 0 
  64a   +16b   +4c   +d    = 0 
  a   +b   +c   +d    = 3 
  6a   +2b          = 0 

So formt man das Gleichungssystem um:
  8a   +4b   +2c   +d    = 0 
  64a   +16b   +4c   +d    = 0 
  a   +b   +c   +d    = 3 
  6a   +2b          = 0 
  8a   +4b   +2c   +d    = 0 
  64a   +16b   +4c   +d    = 0 
  a   +b   +c   +d    = 3 
     -4b   -6c   -6d    = -18 
 ( das -6-fache der dritten Zeile wurde zur vierten Zeile addiert )
  8a   +4b   +2c   +d    = 0 
  64a   +16b   +4c   +d    = 0 
     0,75b   +0,938c   +0,984d    = 3 
     -4b   -6c   -6d    = -18 
 ( das -0,016-fache der zweiten Zeile wurde zur dritten Zeile addiert )
  8a   +4b   +2c   +d    = 0 
     -16b   -12c   -7d    = 0 
     0,75b   +0,938c   +0,984d    = 3 
     -4b   -6c   -6d    = -18 
 ( das -8-fache der ersten Zeile wurde zur zweiten Zeile addiert )
  a   +0,5b   +0,25c   +0,125d    = 0 
     -16b   -12c   -7d    = 0 
     0,75b   +0,938c   +0,984d    = 3 
     -4b   -6c   -6d    = -18 
 ( die erste Zeile wurde durch 8 geteilt )
  a   +0,5b   +0,25c   +0,125d    = 0 
     -16b   -12c   -7d    = 0 
     0,75b   +0,938c   +0,984d    = 3 
        -1c   -0,75d    = -2 
 ( das 5,333-fache der dritten Zeile wurde zur vierten Zeile addiert )
  a   +0,5b   +0,25c   +0,125d    = 0 
     -16b   -12c   -7d    = 0 
        0,375c   +0,656d    = 3 
        -1c   -0,75d    = -2 
 ( das 0,047-fache der zweiten Zeile wurde zur dritten Zeile addiert )
  a   +0,5b   +0,25c   +0,125d    = 0 
     b   +0,75c   +0,438d    = 0 
        0,375c   +0,656d    = 3 
        -1c   -0,75d    = -2 
 ( die zweite Zeile wurde durch -16 geteilt )
  a   +0,5b   +0,25c   +0,125d    = 0 
     b   +0,75c   +0,438d    = 0 
        0,375c   +0,656d    = 3 
           d    = 6 
 ( das 2,667-fache der dritten Zeile wurde zur vierten Zeile addiert )
  a   +0,5b   +0,25c   +0,125d    = 0 
     b   +0,75c   +0,438d    = 0 
        c   +1,75d    = 8 
           d    = 6 
 ( die dritte Zeile wurde durch 0,375 geteilt )


vierte Zeile:
      d   =  6

dritte Zeile:
    c  +1,75d   =  8
Schon berechnete Variablen einsetzen:  
    c  +1,75⋅6   =  8
Nach c freistellen: c = -2,5

zweite Zeile:
  b  +0,75c  +0,438d   =  0
Schon berechnete Variablen einsetzen:  
  b  +0,75⋅(-2,5)  +0,438⋅6   =  0
Nach b freistellen: b = -0,75

erste Zeile:
a  +0,5b  +0,25c  +0,125d   =  0
Schon berechnete Variablen einsetzen:  
a  +0,5⋅(-0,75)  +0,25⋅(-2,5)  +0,125⋅6   =  0
Nach a freistellen: a = 0,25

Einsetzen liefert also, dass die Funktion gleich 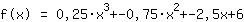f(x)=1*0.25*x^3+1*-0.75*x^2+1*-2.5*x+1*6 ist.



Und wie wende ich das alles auf mein Beispiel an?

Gib doch einfach oben deine Aufgabe ein und lass dir zeigen, wie man das anwendet. Oder denke dir irgendeine interessante Aufgabe aus und schau mal, was Mathepower macht.