Was ist eine lineare Funktion?
Eine lineare Funktion ist eine Funktion, deren Graph eine Gerade ist. Beispiel:
Deine Funktion: 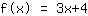
Hier siehst du den Graphen deiner Funktion.
|
|
- Nullstellen bei -1.333
- y-Achsenabschnitt bei (0|4)
|
Der Funktionsgraph einer linearen Funktion ist immer eine Gerade.
Ein anderes Wort für lineare Funktion ist übrigens lineare Zuordnung.
Was ist die Steigung einer linearen Funktion?
Die Steigung einer linearen Funktion entspricht der Zahl vor dem x. Sie gibt an, wie viele Kästchen man nach oben / unten gehen muss, wenn man ein Kästchen nach rechts geht. Beispiel:
Deine Funktion: 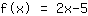
Hier siehst du den Graphen deiner Funktion.
|
|
- Nullstellen bei 2.5
- y-Achsenabschnitt bei (0|-5)
|
Wie wir sehen, hat die Funktion die Steigung
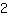
. Wenn man von einem beliebigen Punkt auf dem Funktionsgraphen ein Kästchen nach rechts geht, muss man zwei Kästchen nach oben gehen, um wieder auf dem Graphen der Funktion zu sein.
Noch ein Beispiel, diesmal mit negativer Steigung:
Deine Funktion: 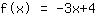
Hier siehst du den Graphen deiner Funktion.
|
|
- Nullstellen bei 1.333
- y-Achsenabschnitt bei (0|4)
|
Diese lineare Funktion hat die Steigung
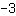
. Das heißt, immer, wenn wir ein Kästchen nach rechts gehen, müssen wir drei Kästchen nach unten gehen, um wieder auf dem Graphen der linearen Funktion zu sein.
Was ist der y-Achsenabschnitt einer linearen Funktion?
Der y-Achsenabschnitt ist die Zahl am Ende der linearen Funktion. Er gibt an (wie der Name schon sagt...), wo der Funktionsgraph die y-Achse schneidet. Wenn man sich die beiden Funktionsgraphen oben anschaut, sieht man, dass
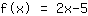
die y-Achse bei
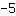
schneidet und
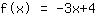
die y-Achse bei
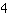
schneidet.
Wie kann man die Funktionsgleichung aus der Steigung und einem Punkt berechnen?
Dazu muss man den Punkt in die Funktionsgleichung einsetzen, soll heißen: die vordere Koordinate für x und die hintere für f(x) einsetzen. Hier mal ein Beispiel: Angenommen, wir wissen, dass unsere Funktion die Steigung
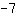
haben und durch den Punkt (-2|5) verlaufen soll.
Deine Eingaben:
Punkt (-2|5); Steigung -7;
Deine Funktion: 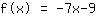
Hier siehst du den Graphen deiner Funktion.
|
|
- Nullstellen bei -1.286
- y-Achsenabschnitt bei (0|-9)
Mathepower hat wie folgt gerechnet:
y-Achsenabschnitt b durch Einsetzen bestimmen:
Allgemeine Form der linearen Funktion: f(x)=mx+b
Setze 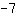 für m, für m, 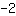 für x und für x und 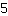 für f(x) ein. für f(x) ein.
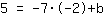 | | | Multipliziere 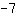 und und 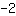 |
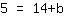 | | | Vertausche beide Seiten der Gleichung. |
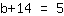 | | | 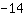 |
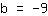 | | |
Also ist der y-Achsenabschnitt gleich 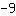
Funktionsgleichung also: 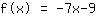
|
Wie kann man die Gleichung einer linearen Funktion aus zwei Punkte berechnen?
Dazu berechnet man zunächst die Steigung m, wobei man die x- und y- Koordinaten der beiden Punkte in die Formel
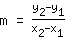
einsetzt. Soll heißen: Man berechnet den Abstand der beiden y-Koordinaten und teilt ihn durch den Abstand der beiden x-Koordinaten. Hier mal ein Beispiel:
Deine Eingaben:
Punkt (1|2); Punkt (3|8);
Deine Funktion: 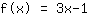
Hier siehst du den Graphen deiner Funktion.
|
|
- Nullstellen bei 0.333
- y-Achsenabschnitt bei (0|-1)
Mathepower hat wie folgt gerechnet:
m berechnen: Verwende die Formel 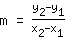 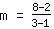 | | | addiere  und und 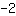 |
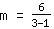 | | | addiere 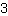 und und 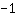 |
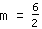 | | | Teile 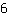 durch durch 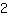 |
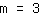 | | |
y-Achsenabschnitt b durch Einsetzen bestimmen:
Allgemeine Form der linearen Funktion: f(x)=mx+b
Setze 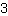 für m, für m, 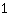 für x und für x und 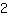 für f(x) ein. für f(x) ein.
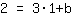 | | |
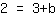 | | | Vertausche beide Seiten der Gleichung. |
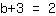 | | | 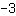 |
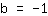 | | |
Also ist der y-Achsenabschnitt gleich 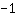
Funktionsgleichung also: 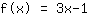
|
Wie man sieht, hat man zunächst nur die Steigung berechnet. Um dann die Funktionsgleichung zu ermitteln, muss man noch einen Punkt einsetzen und erhält eine Gleichung, mit der man den y-Abschnitt bestimmen kann. lineare, funktionen, mathe, gleichungen, formel, aufgaben, zuordnung, beispiele, funktionsgleichung, steigung, gleichung, zeichnen, wertetabelle, nullstellen
Kann ich dazu noch mehr Beispiele sehen?
Klar, gib deine eigenen Beispiele einfach oben ein und sie werden dir sofort kostenlos ausgerechnet. (Das ist eigentlich das Konzept von Mathepower:
Du schaust dir nicht nur irgendwelche vorgerechneten Beispiele mit Erklärungen an, sondern darfst dir sogar selbst die Beispiele aussuchen.)