Dreieck

Dieses Skript berechnet aus drei beliebigen Angaben eines Dreieckes alle weiteren.
Drei Felder sind auszufüllen. Rest wird berechnet.
Hinweis: Dieses Script kann noch nicht alle Eingaben verarbeiten.

a: b: c:
alpha: beta: gamma:
Höhen:
h a: h b: h c:
Schwerelinie:
s a: s b: s c:
Winkelhalbierende:
w a: w b: w c:
Flächeninhalt:

Du hast Mathefragen? Schau immer erst bei Mathepower.com!

Für Dreiecke gilt:
Sinussatz :
a / b = sin alpha / sin beta
Kosinussatz :
a² = b² + c² - 2bc cos alpha

Dreiecke

Was ist ein Dreieck?

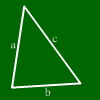
Hier sehen wir ein Dreieck.
Ein Dreieck hat drei Seiten und drei Ecken.
An jeder der Ecken befindet sich ein Innenwinkel, also der Winkel, der von den zwei an der Ecke endenden Seiten eingeschlossen wird.
Die Summe aller Innenwinkel in einem Dreieck ist stets gleich 180 Grad.

Durch welche Angaben ist ein Dreieck eindeutig bestimmt?

Ein Dreieck ist stets durch Angabe von drei Seiten eindeutig bestimmt, außerdem durch Angabe zweier Winkel und einer Seite, oder durch zwei Seiten und den Winkel zwischen diesen Seiten.
Es gibt auch andere Fälle, in denen ein Dreieck durch drei Angaben eindeutig bestimmt ist, jedoch nicht immer; z.B. gibt es zu zwei gegebenen Seiten und einer gegebenen Höhe auf einer Seite stets zwei Möglichkeiten, wie man das Dreieck konstruieren kann. Jedoch gibt es zu drei gegebenen Angaben bei einem Dreieck nie mehr als zwei Möglichkeiten, wie man aus ihnen ein Dreieck konstruieren kann.

Was ist die Höhe eines Dreieckes?

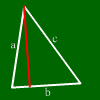
Die Höhe ist die Länge der Strecke, die auf einer Seite senkrecht steht und zur gegenüberliegenden Ecke verläuft.

Welche Berechnungen kann man an einem Dreieck durchführen?

Den Flächeninhalt eines Dreieckes berechnet man, indem man eine beliebige Seite und die Höhe auf dieser Seite betrachtet. Der Flächeninhalt ist dann gleich (Seite*Höhe)/2.
Die Seiten und Winkel kann man mit Hilfe von Sinus und Kosinus (Thema Klasse 10) berechnen: Es gilt nämlich für zwei Seiten a und b und die gegenüberliegenden Winkel Alpha und Beta:
a/sin Alpha = b/sin Beta (Sinussatz).
Weiter gilt für drei Seiten a,b,c und den Winkel Gamma gegenüber von Seite c:
a²=b²+c²-2*b*c*cos Gamma (Kosinussatz).

Welche interessanten Linien gibt es bei Dreiecken?

Interessante Linien am Dreieck sind die Mittelsenkrechten, die Winkelhalbierenden, die Schwerelinien und die Höhen.

Welche Spezialfälle von Dreiecken sind interessant?

Interessante Spezialfälle sind das gleichseitige Dreieck, das gleichschenklige Dreieck und das rechtwinklige Dreieck.

Wie konstruiert man den Umkreis von einem Dreieck?

Um den Umkreis von einem Dreieck zu konstruieren, konstruiert man auf jeder Seite die Mittelsenkrechte, oder nur zwei dieser Mittelsenkrechten, da sie sich ja schließlich alle drei in einem Punkt schneiden. Dann zeichnet man um diesen Punkt einen Kreis, der bei einem der Eckpunkte beginnt. Dieser Kreis ist dann der Umkreis von dem Dreieck.

Dafür haben wir auch eine Flash-Animation:

Wie konstruiert man den Inkreis von einem Dreieck?

Um den Inkreis von einem Dreieck zu konstruieren, konstruiert man die drei Winkelhalbierenden. Zieht man um den Winkelhalbierendenschnittpunkt nun einen Kreis, der eine der Seiten von dem Dreieck als Tangente hat, so ist das genau der Inkreis.

Auch dafür haben wir eine Flash-Animation:

Wie konstruiert man den Schwerpunkt von einem Dreieck?

Um den Schwerpunkt von einem Dreieck zu konstruieren, konstruiert man die drei Schwerelinien. Dies sind die Strecken von einem Seitenmittelpunkt zur gegenüberliegenden Ecke. Sie schneiden sich in einem Punkt; dies ist der Schwerpunkt.

Die folgende Flash-Animation zeigt das Verfahren:

Für weitere Infos bewege die Maus über eines der unten stehenden Wörter, und das entsprechende Stück wird auf dem Dreieck unten farbig markiert.

Seite a, Seite b, Seite c
Winkel Alpha, Winkel Beta, Winkel Gamma
Höhe auf a, Höhe auf b, Höhe auf c
Schwerelinie auf a, Schwerelinie auf b, Schwerelinie auf c
Winkelhalbierende zu Alpha, Winkelhalbierende zu Beta, Winkelhalbierende zu Gamma
Flächeninhalt

Gefällts dir hier? Mathepower zu den Favoriten hinzufügen und wiederkommen!