Wofür braucht man das Vorzeichenwechselkriterium?
Um zu unterscheiden, ob eine Funktion, deren
Ableitung 
ist, einen
Hochpunkt, einen Tiefpunkt oder einen Sattelpunkt hat. Drei Beispiele, in denen die Funktion jeweils im Punkt (1|2) die Steigung

hat:
Diese Funktion hat bei (1|2) Steigung

und einen Hochpunkt. Bei
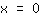
steigt der Graph, sprich, die Ableitung ist hier größer als

. Bei
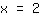
fällt der Graph, sprich, die Ableitung ist hier kleiner als

. Hat eine Funktion also einen Hochpunkt, dann ist vor diesem Hochpunkt das Vorzeichen der Ableitung ein + und dahinter ein -. Die Ableitung macht also einen
Vorzeichenwechsel von + nach -.
Diese Funktion hat bei (1|2) Steigung

, aber einen Tiefpunkt. Bei
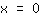
fällt der Graph, sprich, die Ableitung ist hier kleiner als

. Bei
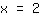
steigt der Graph, sprich, die Ableitung ist hier größer als

. Hat eine Funktion also einen Tiefpunkt, dann ist vor diesem Tiefpunkt das Vorzeichen der Ableitung ein - und dahinter ein +. Die Ableitung macht also einen Vorzeichenwechsel von - nach +.
Diese Funktion hat ebenfalls bei (1|2) Steigung

, aber weder einen Hoch- noch einen Tiefpunkt. Man sieht, dass der Graph sowohl bei
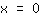
als auch bei
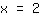
steigt. Macht die Ableitung keinen Vorzeichenwechsel, dann hat man offenbar keinen Extrempunkt. Einen solchen Punkt (der kein Extrempunkt ist, aber trotzdem Ableitung

hat) nennt man Sattelpunkt.
Wie wende ich das Vorzeichenwechselkriterium an?
- Zuerst leitest du deine Funktion ab.
- Dann bestimmst du die Nullstellen der Ableitung. Nur diese Nullstellen können x-Koordinaten von Hoch- oder Tiefpunkten sein.
- Als letztes setzt du Werte in der Nähe der Nullstellen in die Ableitung ein. Macht die Ableitung in der Nähe der Nullstelle einen Vorzeichenwechsel, so hast du einen Extrempunkt gefunden. Sonst nicht.
Wieso heißt das Vorzeichenwechselkriterium hinreichendes Kriterium?
Dass die Ableitung gleich  ist, ist notwendig für einen Extrempunkt (soll heißen: muss an einem Extrempunkt so sein). Es ist aber nicht hinreichend für einen Extrempunkt, was da heißt, nur weil die Ableitung
ist, ist notwendig für einen Extrempunkt (soll heißen: muss an einem Extrempunkt so sein). Es ist aber nicht hinreichend für einen Extrempunkt, was da heißt, nur weil die Ableitung  ist, muss man noch lange keinen Extrempunkt haben (siehe oben beim Sattelpunkt).
ist, muss man noch lange keinen Extrempunkt haben (siehe oben beim Sattelpunkt).
Wenn die Ableitung aber nicht nur  ist, sondern sogar einen Vorzeichenwechsel macht, dann muss man einen Extrempunkt haben. Man sagt in der Mathematik, Ableitung
ist, sondern sogar einen Vorzeichenwechsel macht, dann muss man einen Extrempunkt haben. Man sagt in der Mathematik, Ableitung  und Vorzeichenwechsel ist hinreichend dafür, dass wir sicher sagen können, hier ist ein Extrempunkt.
und Vorzeichenwechsel ist hinreichend dafür, dass wir sicher sagen können, hier ist ein Extrempunkt.
Kann ich mal eine Beispielaufgabe sehen?
Klar.
Ableiten der Funktion 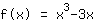
| ( Ableitung von  ) + ( Ableitung von ) + ( Ableitung von 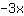 ) ) | | Die Ableitung von 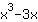 ist also ist also 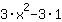 . . | |
Ableitung vereinfachen:
Also lautet die erste Ableitung: 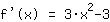
Zweite Ableitung, also Ableitung der Funktion 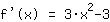 :
:
| ( Ableitung von 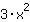 ) + ( Ableitung von ) + ( Ableitung von 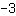 ) ) | | Die Ableitung von 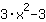 ist also ist also 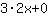 . . | |
Ableitung vereinfachen:
Also lautet die zweite Ableitung: 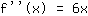
Dritte Ableitung, also Ableitung der Funktion 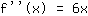 :
:
Also lautet die dritte Ableitung: 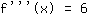
Extrempunkte gesucht.
Notwendiges Kriterium: Nullstellen der ersten Ableitung finden.
Nullstellen gesucht von 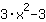
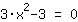 | | |
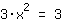 | | ( Bringe 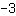 negativ auf die andere Seite. ) negativ auf die andere Seite. ) |
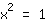 | | ( Teile auf beiden Seiten durch 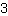 ) ) |
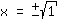 | | ( Auf beiden Seiten Quadratwurzel ziehen. ) |
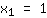 | | ( Ziehe die Wurzel aus 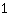 ) ) |
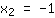 | | ( Ziehe die Wurzel aus 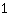 ) ) |
mögliche Extremstellen bei {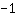 ;
;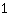 }
}
Vorzeichenwechsel-Kriterium: Ist bei 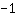 ein Extrempunkt?
ein Extrempunkt?
Setze -2 und 0 in die erste Ableitung ein.
Wert -2 in 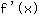 einsetzen:
einsetzen:
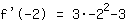 | | |
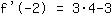 | | ( Rechne 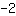 hoch hoch 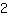 aus. ) aus. ) |
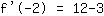 | | ( Multipliziere 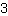 und und 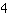 ) ) |
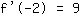 | | ( addiere 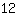 und und 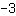 ) ) |
Wert 0 in 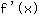 einsetzen:
einsetzen:
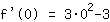 | | |
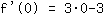 | | ( Rechne  hoch hoch 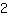 aus. ) aus. ) |
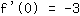 | | ( Multipliziere 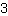 und und  ) ) |
Vorzeichenwechsel von + nach -, also wird bei 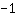 ein Maximum angenommen.
ein Maximum angenommen.
Wert -1 in 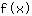 einsetzen:
einsetzen:
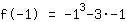 | | |
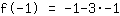 | | ( Rechne 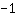 hoch hoch 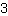 aus. ) aus. ) |
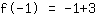 | | ( Multipliziere 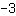 und und 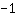 ) ) |
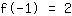 | | ( addiere 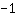 und und 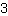 ) ) |
Hochpunkt (-1|2)
Vorzeichenwechsel-Kriterium: Ist bei 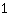 ein Extrempunkt?
ein Extrempunkt?
Setze 0 und 2 in die erste Ableitung ein.
Wert 0 in 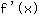 einsetzen:
einsetzen:
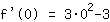 | | |
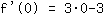 | | ( Rechne  hoch hoch 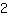 aus. ) aus. ) |
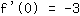 | | ( Multipliziere 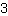 und und  ) ) |
Wert 2 in 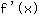 einsetzen:
einsetzen:
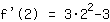 | | |
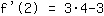 | | ( Rechne 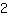 hoch hoch 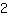 aus. ) aus. ) |
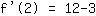 | | ( Multipliziere 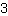 und und 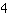 ) ) |
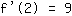 | | ( addiere 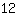 und und 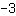 ) ) |
Vorzeichenwechsel von - nach +, also wird bei 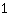 ein Minimum angenommen.
ein Minimum angenommen.
Wert 1 in 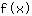 einsetzen:
einsetzen:
Tiefpunkt (1|-2)
Kann ich noch eine Beispielaufgabe sehen?
Jep, das hier ist Mathepower. Gib oben doch einfach deine eigene Beispielaufgabe ein und sie wird genauso gelöst.