Was ist eine Kurvendiskussion?
Bei einer
Kurvendiskussion bestimmt man sämtliche charakteristischen Punkte einer Funktion, also
Nullstellen, y-Achsenschnittpunkt, Hoch- und Tiefpunkte,
Wendepunkt.
Wie bestimmt man diese Punkte?
Man bestimmt zuerst die erste, zweite und dritte
Ableitung der Funktion. Dann setzt man die Funktion sowie diese Ableitung gleich Null: Nullstellen sind Lösungen der
Gleichung 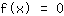
.
Extrempunkte können nur an Nullstellen der Ableitungsfunktion sein, also muss man die Gleichung
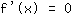
lösen, um mögliche Extrempunkte zu finden. (ob an einer Nullstelle der Ableitung wirklich ein Extrempunkt ist, kann man mit dem
Vorzeichenwechselkriterium testen.) An einem Wendepunkt muss die zweite Ableitung gleich

sein, also ist, um einen Wendepunkt zu finden, die Gleichung
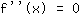
zu lösen.
Wieso werden Kurvendiskussionen in der Schule nicht mehr so viel geübt?
Eigentlich sind Kurvendiskussionen ein wenig sinnlos: Man rechnet stur nach Verfahren alle möglichen Punkte eines Funktionsgraphen aus, ohne darüber nachzudenken, was diese anschaulich bedeuten. Deswegen werden heutzutage Aufgaben immer wichtiger, in denen man nicht nur stur alle möglichen Punkte ausrechnet, sondern auch mal überlegt, was diese Punkte in Anwendungskontexten bedeuten.
Kann ich mal ein Beispiel sehen?
Ja, schauen wir uns mal die Kurvendiskussion der Funktion
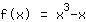
an.
Mathepower rechnet mit dieser Funktion:
Hier siehst du den Graphen deiner Funktion.
|
|
- Nullstellen bei -1; 0; 1
- y-Achsenabschnitt bei (0|0)
- Hochpunkte, Tiefpunkte bei (-0.577|0.385); (0.577|-0.385)
- Wendepunkte bei (0|0)
Mathepower hat wie folgt gerechnet:
Nullstellen:
Nullstellen gesucht von 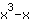
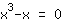 | | | Klammere  aus. aus. |
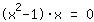 | | |  | | | Produkt Null. Also ist entweder der Faktor 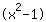 gleich Null... gleich Null... |
 | | | +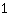 |
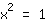 | | | Auf beiden Seiten Quadratwurzel ziehen. |
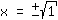 | | | 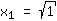 | | | Ziehe die Wurzel aus 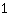 |
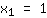 | | | 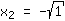 | | | Ziehe die Wurzel aus 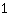 |
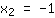 | | | 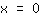 | | | ... oder der Faktor 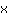 ist gleich Null ist gleich Null |
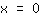 | | |
Nullstellen sind also: {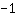 ; ; ; ;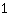 } }
Symmetrie:
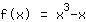 ist punktsymmetrisch zum Ursprung. ist punktsymmetrisch zum Ursprung.
y-Achsenabschnitt: 0 in die Funktion einsetzen
Wert 0 in 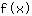 einsetzen: einsetzen:
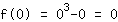
Also: y-Achsenabschnitt bei (0|0)
Ableiten der Funktion 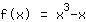
| 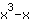 ableiten: ableiten: | ( Ableitung von  ) ) | + | ( Ableitung von 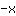 ) ) | 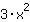 | + | 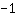 |
Die Ableitung von 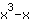 ist also ist also 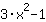 . . |
| |
|
Also lautet die erste Ableitung: 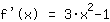
Zweite Ableitung, also Ableitung der Funktion 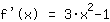 : :
| 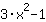 ableiten: ableiten: | ( Ableitung von 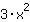 ) ) | + | ( Ableitung von 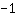 ) ) | 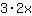 | + |  |
Die Ableitung von 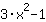 ist also ist also 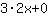 . . |
| |
|
Ableitung vereinfachen:
Also lautet die zweite Ableitung: 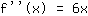
Dritte Ableitung, also Ableitung der Funktion 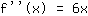 : :
Ableitung von 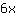 ist ist 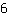
Also lautet die dritte Ableitung: 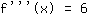
Extrempunkte gesucht.
Notwendiges Kriterium: Nullstellen der ersten Ableitung finden.
Nullstellen gesucht von 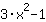
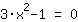 | | | +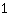 |
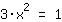 | | | : 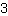 |
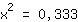 | | | Auf beiden Seiten Quadratwurzel ziehen. |
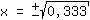 | | | 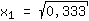 | | | Ziehe die Wurzel aus  |
 | | | 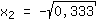 | | | Ziehe die Wurzel aus  |
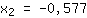 | | |
mögliche Extremstellen bei {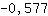 ; ;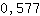 } }
Nullstellen der ersten Ableitung in zweite einsetzen:
Wert -0.577 in 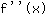 einsetzen: einsetzen:
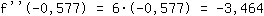
-3.464 ist kleiner als 0. Bei 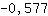 wird also ein Maximum angenommen. wird also ein Maximum angenommen.
Wert -0.577 in 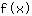 einsetzen: einsetzen:
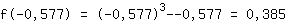
Hochpunkt (-0.577|0.385)
Wert 0.577 in 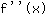 einsetzen: einsetzen:

3.464 ist größßer als 0. Bei 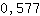 wird also ein Minimum angenommen. wird also ein Minimum angenommen.
Wert 0.577 in 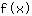 einsetzen: einsetzen:
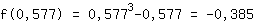
Tiefpunkt (0.577|-0.385)
Wendepunkte gesucht.
Notwendiges Kriterium: Nullstellen der zweiten Ableitung finden.
Nullstellen gesucht von 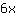
mögliche Wendepunkte bei { } }
Nullstellen der zweite Ableitung in dritte einsetzen:
Da in der dritten Ableitung gar kein x mehr vorkommt, ergibt das Einsetzen 6.
6 ist größßer als 0. Bei  ist also ein Wendepunkt rechts->links. ist also ein Wendepunkt rechts->links.
Wert 0 in 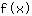 einsetzen: einsetzen:
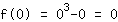
Wendepunkt (0|0)
|