Der kgv zweier Zahlen ist deren kleinstes gemeinsames Vielfaches, also die kleinste Zahl, die durch beide Zahlen teilbar ist.
Wofür braucht man das kgv?
Zum Beispiel, wenn man zwei Brüche gleichnamig machen will. Der kleinste mögliche gemeinsame Nenner der beiden Brüche ist das kgV der beiden Nenner.
Beispiel: Angenommen, man will
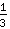
mit
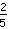
vergleichen. Erst einmal ist gar nicht klar, welcher der Brüche größer ist. Aber man kann sich überlegen: Das kgV von
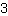
und
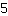
ist
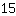
. Also kann man beide Brüche so
erweitern, dass sie den Nenner
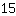
haben:
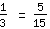
und
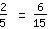
.
Also ist
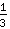
weniger als
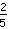
, was man leicht sieht, wenn man sie erweitert.
KGV - kleinstes gemeinsames Vielfaches
Dieses Programm berechnet das kleinste gemeinsame Vielfache zweier Zahlen. Einfach Zahlen eingeben und kgV ausrechnen lassen.