Comment résoudre des équations linéaires de base?
Tout d'abord, jetez un il à cet exemple:
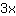
-
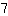
+
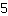
= x +
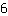
On commence en simplifiant les deux membres. Sur le membre gauche, vous pouvez additionner
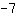
et
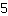
. Ensuite, vous obtenez l'équation:
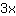
-

= x +
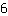
Ensuite, vous devez réorganiser l'équation de telle manière que les termes avec x soient isolés sur un membre et les nombres sur l'autre. Puisque nous n'aimons pas la x à droite, nous soustrayons x aux deux membres. Alors,
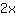
reste sur le côté gauche.
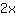
-

=
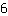
Maintenant, on porte le nombre

de l'autre côté. Nous ajoutons donc

sur les deux côtés. Puisque
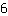
+

=

, on obtient
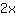
=

Enfin, nous divisons les deux côtés par le coefficient de x:
X =
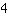
L'équation est maintenant résolue, dont
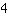
est la solution.
De la même manière, vous pouvez toujours procéder: tout d'abord, simplifiez autant que possible les deux côtés de l'équation. Simplifiez ensuite avec les principes d'équivalence: additionner ou soustraire avec conscience un nombre dans les membres. Enfin, il devrait y avoir un terme multiple de l'inconnue dans un membre et un terme constant dans l'autre. Pour obtenir le résultat, il faut simplement diviser par le nombre devant la variable et l'équation est résolue.
Comment Mathepower présente-t-il les solutions?
Lorsque vous avez entré une équation, vous obtenez ceci:
| Votre exercice: | | Explication pas à pas: |
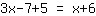 | | | ajouter 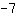 et et 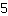 |
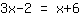 | | | 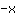 |
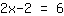 | | | + |
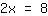 | | | :  |
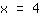 | | |
Ensemble de solutions: {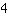 } } |
Et si je veux qu'une autre équation soit résolue?
Vous êtes sur mathepower.com. Entrez votre équation ci-dessus et elle sera résolue dans la même procédure. Immédiatement et gratuitement (Mathepower est financé par la publicité).
Quels cas particuliers doivent être pris en compte lors de la résolution d'équations?
Les cas particuliers les plus importants sont quand l'équation a un nombre infini de solutions (indéterminée) ou aucune solution (impossible).
On voit d'abord un exemple d'une équation indéterminée, c'est-à-dire quand tout x réel est solution:
| Votre exercice: | | Explication pas à pas: |
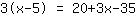 | | | Développer 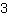 et et 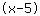 . . |
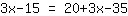 | | | ajouter 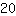 et et 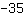 |
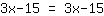 | | | 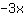 |
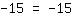 | | | | L'équation est indéterminée, il existe une infinité de solutions. |
|
Ensemble de solutions: R |
Vous voyez que vous vous retrouvez avec les mêmes valeurs dans les deux membres. C'est évidemment une identité, vérifiée pour toute valeur de x (il n'y a quand même plus de x dans cette équation). Ainsi, nous avons vu comme une équation peut avoir un nombre infini de solutions.
Qu'est-ce que cela signifie lorsqu'une équation a un nombre infini de solutions? Vous pouvez l'essayer: prenez n'importe quelle valeur pour x (par exemple
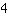
, les deux membres seront les mêmes. Cela fonctionne avec n'importe quelle valeur pour x. La raison en est que les termes des deux membres sont équivalents (d'ici identité), c'est-à-dire des termes avec la même solution avec n'importe quelle valeur pour x.
L'autre cas spécial est avec une équation impossible, c'est-à-dire sans solution:
| Votre exercice: | | Explication pas à pas: |
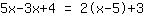 | | | ajouter 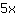 et et 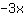 |
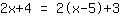 | | | Développer  et et 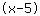 . . |
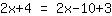 | | |
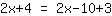 | | | ajouter 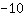 et et 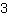 |
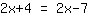 | | | 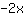 |
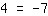 | | | | L'équation est impossible, n'a pas de solutions. |
|
Ensemble de solutions: {} |
On voit qu'il n'y a pas de x dans l'équation après réarrangement et que l'équation est évidemment fausse. Cela est dû au fait que l'équation d'origine n'a pas de solution.