Que signifie faire l'étude d'une fonction?
L'étude de fonction est un calcul pour trouver tous les points caractéristiques d'une fonction, par exemple les intersections avec l'axe des ordonnées y et des abscisses x (c'est-à-dire les racines), les points tournant maximal et minimal et points d'inflexion.
Comment on obtient ces points?
On commence en calculant les premières trois dérivées. Ensuite, vous définissez la fonction, ainsi que les dérivées, égale à zéro: les racines sont des solutions de l'équation
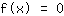
. Les points tournants peuvent être calculés seulement avec les racines de la fonction dérivée, c'est-à-dire en résolvant l'équation
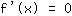
pour trouver les points tournants maximal et minimal. À un point d'inflexion, la dérivée deuxième doit être

, donc pour trouver des points d'inflexion, il faut résoudre l'équation
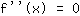
(Afin de vérifier quel type de point stationnaire on a, on pourrait utiliser le critère de changement de signe).
Pourquoi l'étude des fonctions se fait-il moins approfondie de nos jours?
C'est un peu inutile faire l'étude d'une fonction quand ça consiste d'apprendre à effectuer des calculs ponctuels à chaque fois sans trop réfléchir à leur signification. Par conséquent, les exercices où doit penser à la signification des points critique d'une fonction deviennent plus important de nos jours.
Puis-je jeter un coup d'œil à un exemple?
Bien sûr. Permet d'étudier la fonction qui vient
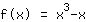
.
Mathepower travaille avec cette fonction:
Ceci est le graphique de votre fonction.
|
|
- Racines à -1; 0; 1
- Ordonnée à l'origine à (0|0)
- Points tournants maximal/minimal à (-0.577|0.385); (0.577|-0.385)
- Points d'inflexion à (0|0)
Voici ce que Mathepower a calculé:
Les points stationnaires:
À la recherche des racines de 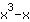
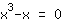 | | | Factoriser 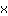 . . |
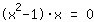 | | | 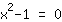 | | | Loi du produit-nul: donc ou le facteur 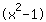 doit être nul…. doit être nul…. |
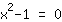 | | | + |
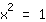 | | | On applique la fonction racine carrée dans les deux membres de l'équation. |
 | | |  | | | Extraire la racine de  |
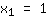 | | |  | | | Extraire la racine de  |
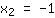 | | | 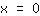 | | | … ou le facteur 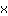 doit être nul doit être nul |
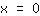 | | |
Donc, les points stationnaires sont: { ; ; ; ; } }
Symétrie:
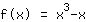 est symétrique ponctuellement par rapport à l'origine. est symétrique ponctuellement par rapport à l'origine.
intersection avec l'axe des ordonnées: on insère x = 0 dans la fonction
Insérer 0 dans la fonction 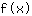 : :
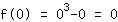
Ainsi, l'ordonnée à l'origine est (0|0)
Dériver la fonction 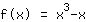
| Dériver la fonction 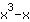 : : | ( Dérivé de  ) ) | + | ( Dérivé de 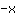 ) ) | 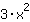 | + |  |
Ainsi, la dérivée de 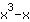 est est 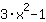 . . |
| |
|
Donc, la dérivée première est: 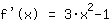
Dérivée seconde, c'est-à-dire la dérivée de f', est: 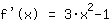 : :
| Dériver la fonction 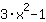 : : | ( Dérivé de 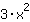 ) ) | + | ( Dérivé de  ) ) | 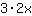 | + |  |
Ainsi, la dérivée de 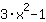 est est 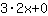 . . |
| |
|
Simplifiez la dérivation:
Donc, la dérivée seconde est: 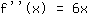
Dérivée troisième, c'est-à-dire la dérivée de f'', est: 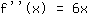 : :
La dérivée de 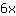 est est 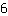
Donc, la dérivée troisième est: 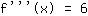
À la recherche de points tournants.
Critère important: nous devons trouver les racines de la dérivée première.
À la recherche des racines de 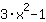
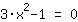 | | | + |
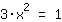 | | | : 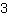 |
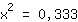 | | | On applique la fonction racine carrée dans les deux membres de l'équation. |
 | | |  | | | Extraire la racine de  |
 | | |  | | | Extraire la racine de  |
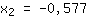 | | |
Probables points tournants in: {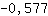 ; ;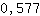 } }
Insérez les racines de la dérivée première dans la dérivée seconde:
Insérer -0.577 dans la fonction 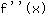 : :
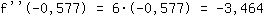
-3.464 est plus petit que 0. Il y a donc un maximum en 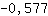 . .
Insérer -0.577 dans la fonction 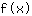 : :
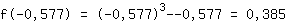
Point tournant maximal (-0.577|0.385)
Insérer 0.577 dans la fonction 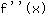 : :

3.464 , qui est plus grand que 0. Il y a donc un minimum en 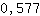 . .
Insérer 0.577 dans la fonction 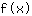 : :
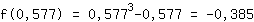
Point tournant minimal (0.577|-0.385)
Recherche de points d'inflexion obliques.
Critère important: il faut trouver les racines de la dérivée seconde.
À la recherche des racines de 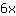
Probables points d'inflexion obliques en { } }
Insérez les racines de la dérivée seconde dans la dérivée troisième:
La dérivée troisième ne contient plus la variable x , donc l'insertion de la racine donne 6
6 , qui est plus grande que 0, il y a donc un point d'inflexion croissant (courbure concave -> convexe) en  . .
Insérer 0 dans la fonction 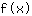 : :
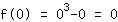
Point d'inflexion oblique (0|0)
|