Comment transformer le graphe d'une fonction?
Cela dépend de la direction que vous souhaitez transformer. En général, les transformations dans la direction y sont plus faciles que les transformations dans la direction x, comme on le verra.
Comment déplacer une fonction dans la direction y?
Ajoutez simplement à la fonction la valeur que vous souhaitez. Ça y est. Par exemple, on veut déplacer le graphique de la fonction
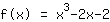
de
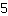
unités vers le haut.
Votre exercice:
La fonction 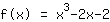 doit être de doit être de
5 unités déplacée vers le haut
Graphique avant du déplacement: :
|
|
La fonction après le déplacement: 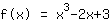
|
|
Voici ce que Mathepower a calculé:
On déplace le graphique de la fonction 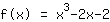 de 5 vers le haut de 5 vers le haut
Ajouter 5 à la fonction.
Fonction déplacée: 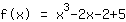
On simplifie le nouveau terme de la fonction: :
|
Comment déplacer une fonction dans la direction x?
Si vous voulez vous déplacer dans la direction x, c'est plus difficile pour deux raisons:
- Vous devez remplacer tous les x par
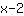
- et faites attention au signe: si vous voulez aller dans la direction croissante x, remplacez x par
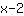 . Mais si vous voulez aller dans la direction opposée, vous remplacez x par
. Mais si vous voulez aller dans la direction opposée, vous remplacez x par 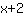 .
.
Voici un autre exemple impliquant cette dernière fonction.
Votre exercice:
La fonction 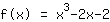 doit être de doit être de
2 unités déplacée vers la droite
Graphique avant du déplacement: :
|
|
La fonction après le déplacement: 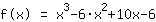
|
|
Voici ce que Mathepower a calculé:
On déplace le graphique de la fonction 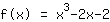 de 2 vers la droite : de 2 vers la droite :
Remplacez chaque x par 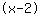
Fonction déplacée: 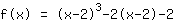
On simplifie le nouveau terme de la fonction: :
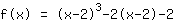 | | | Appliquer l'identité remarquable 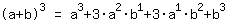 avec a= avec a=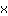 et b= et b= |
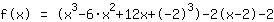 | | | Calculer  élevé à élevé à 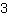 . . |
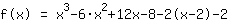 | | | Développer  et et 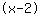 . . |
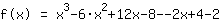 | | |
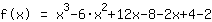 | | | ajouter 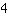 et et  |
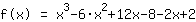 | | | ajouter 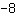 et et  |
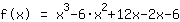 | | | ajouter 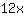 et et 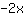 |
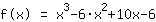 | | |
|
Comment étirer une fonction dans la direction y?
C'est encore une fois facile: multipliez simplement votre fonction entière par le facteur d'étirement. Par exemple, on veut étirer
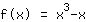
par le facteur

dans la direction y.
Votre exercice:
La fonction 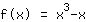 doit être de doit être de
2 dans la direction y unités étirée
Graphique avant du déplacement: :
|
|
La fonction après le déplacement: 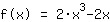
|
|
Voici ce que Mathepower a calculé:
On déplace la fonction 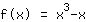 par 2 dans la direction y étirée : par 2 dans la direction y étirée :
On multiplie la fonction par 2
Étirée une fonction 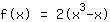
On simplifie le nouveau terme de la fonction: :
|
Comment étirer une fonction dans la direction x?
Encore une fois, comme le déplacement, l'étirement est plus difficile: nous devons remplacer tous les x par
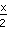
(Attention, ce n'est pas encore la façon dont vous pouvez penser: l'étirement ne signifie pas multipliant par

, mais divisant par
Votre exercice:
La fonction 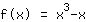 doit être de doit être de
2 dans la direction x unités étirée
Graphique avant du déplacement: :
|
|
La fonction après le déplacement: 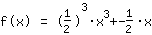
|
|
Voici ce que Mathepower a calculé:
On déplace la fonction 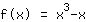 par 2 dans la direction x étirée : par 2 dans la direction x étirée :
Remplacez chaque x par 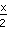
Étirée une fonction 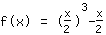
On simplifie le nouveau terme de la fonction: :
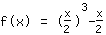 | | | On extrait 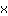 de la fraction de la fraction |
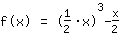 | | | Résolvez avec les propriétés des puissances : 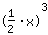 équivaut à équivaut à 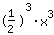 |
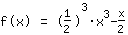 | | | On extrait  de la fraction de la fraction |
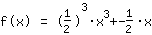 | | |
|
Et si je veux déplacer une autre fonction?
Mathepower est ici pour ça. Entrez votre fonction ci-dessus.