Forme canonique d'une fonction quadratique


Forme canonique

Entrez la fonction à représenter dans la forme canonique.

Astuce: entrez comme 3*x^2.






Qu'est que la forme canonique d'une fonction quadratique?

La forme canonique est une forme spéciale d'une fonction quadratique. Avec cette forme, il est facilement visible où est le point maximum ou minimum (le sommet) de la parabole: le nombre entre parenthèses donne (attention au signe!) la coordonnée x du sommet, le terme connu donne la coordonnée y.

Comment mettre une fonction sous forme canonique?

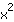
Vous devez utiliser la complétion du carré: pour trouver le terme connu dans le carré (x1) on prend le coefficient de x, on le divise par 2 et on met le résultat au carré (x + x1)^2. Pour faire ça il faut que le coefficient de x^2 soit 1 - sinon on le rend comme ça mais on le verra plus tôt. Voici un exemple:


Mathepower travaille avec cette fonction:

Ainsi, la forme canonique de votre fonction quadratique est f(x)=1*(x+2)^2+-3
Le sommet est en (-2|-3)

Ceci est le graphique de votre fonction.
Dein Browser unterstützt den HTML-Canvas-Tag nicht. Hol dir einen neuen. :P
  • le sommet à (-2|-3)
Voici ce que Mathepower a calculé:
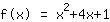f(x)=1*x^2+4*x+1
f(x)=x^2+4*x+(2)^2+-1*(2)^2+1( Complétion du carré )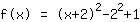
f(x)=(x+2)^2+-1*(2)^2+1( Utilisez l'identité remarquable )
f(x)=(x+2)^2+-3( on simplifie )
f(x)=1*(x+2)^2+-3( on développe )

Comme vous pouvez le voir, la coordonnée x du sommet est égale au nombre entre parenthèses, mais changé de signe (-x1). En outre, on voit à partir de ce calcul qu'il suffit d'utiliser l'identité remarquable à l'envers: passer de la somme remarquable à au produit remarquable. Cela ne fonctionne que s'il y a le bon terme connu (le nombre x1^2 complétant le carré). Il suffit donc d'ajouter le bon nombre et de le soustraire en même temps afin d'obtenir x1^2 plus un autre nombre.

Et s'il y a un coefficient devant le x^2?

Il faut simplement factoriser ce nombre. Exemple:


Mathepower travaille avec cette fonction:
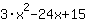=3*x^2+-1*24*x+15

Ainsi, la forme canonique de votre fonction quadratique est f(x)=3*(x+-4)^2+-33
Le sommet est en (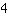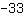4|-33)

Ceci est le graphique de votre fonction.
Dein Browser unterstützt den HTML-Canvas-Tag nicht. Hol dir einen neuen. :P
  • le sommet à (4|-33)
Voici ce que Mathepower a calculé:
f(x)=3*x^2+-24*x+15
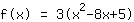f(x)=3*(x^2+-8*x+5)( Factoriser )
f(x)=3*(x^2+-8*x+(-4)^2+-1*(-4)^2+5)( Complétion du carré )
f(x)=3*((x+-4)^2+-1*(-4)^2+5)( Utilisez l'identité remarquable )
f(x)=3*((x+-4)^2+-11)( on simplifie )
f(x)=3*(x+-4)^2+-33( on développe )

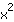
Important: il faut prendre en compte d'abord la factorisation du coefficient de x^2 et compléter le carré par la suite. Sinon, il pourrait y avoir de mauvaises erreurs. (Malheureusement, beaucoup de gens n'y pensent pas et utilisent simplement la formule binomiale même si ce n'est pas encore possible… Dommage que les termes ne peuvent pas crier ""Ouah!"", mais seuls les professeurs de mathématiques peuvent quand ils voient un tel calcul).

Et s'il y a un moins devant le x ^ 2?

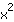
Factorisez simplement -1. À propos: chaque fois qu'il y a un nombre négatif devant le x^2, la parabole est tournée vers le bas. Exemple:


Mathepower travaille avec cette fonction:
=-1*x^2+-1*3*x+2

Ainsi, la forme canonique de votre fonction quadratique est f(x)=-1*(x+3/2)^2+17/4
Le sommet est en (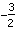-3/2|17/4)

Ceci est le graphique de votre fonction.
Dein Browser unterstützt den HTML-Canvas-Tag nicht. Hol dir einen neuen. :P
  • le sommet à (-1.5|4.25)
Voici ce que Mathepower a calculé:
f(x)=-1*x^2+-3*x+2
f(x)=-1*(x^2+3*x+-2)( Factoriser )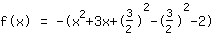
f(x)=-1*(x^2+3*x+(3/2)^2+-1*(3/2)^2+-2)( Complétion du carré )
f(x)=-1*((x+3/2)^2+-1*(3/2)^2+-2)( Utilisez l'identité remarquable )
f(x)=-1*((x+3/2)^2+1*-17/4)( on simplifie )
f(x)=-1*(x+3/2)^2+17/4( on développe )

Et comment est la formule générale de la forme canonique?

Aucun problème pour Mathepower. Entrez simplement la fonction f_f(x)=ax^2+bx+c .


Mathepower travaille avec cette fonction:

Ainsi, la forme canonique de votre fonction quadratique est 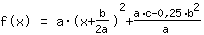f(x)=1*a*(x+b/(2*a))^2+(1*a*c+-0.25*b^2)/a
Le sommet est en (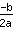(-1*b)/(2*a)|(1*a*c+-0.25*b^2)/a)

Voici ce que Mathepower a calculé:
f(x)=1*a*x^2+1*b*x+1*c
f(x)=1*a*(x^2+b/a*x+c/a)( Factoriser )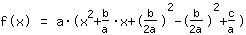
f(x)=1*a*(x^2+b/a*x+(b/(2*a))^2+-1*(b/(2*a))^2+c/a)( Complétion du carré )
f(x)=1*a*((x+b/(2*a))^2+-1*(b/(2*a))^2+c/a)( Utilisez l'identité remarquable )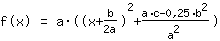
f(x)=1*a*((x+b/(2*a))^2+1*(1*a*c+-0.25*b^2)/a^2)( on simplifie )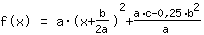
f(x)=1*a*(x+b/(2*a))^2+(1*a*c+-0.25*b^2)/a( on développe )

Puis-je voir encore plus d'exemples?

Bien sûr. Ceci est une calculatrice gratuite pour transformer les fonctions quadratiques en forme canonique. Entrez simplement votre exercice et il sera résolu.