À quoi servent les fractions?
D'abord un exemple: Imaginez que
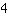
personnes veulent manger un gâteau. Combien de gâteau tout le monde reçoit-il? Bien sûr, le résultat est de

:
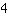
. Mais on le calcule comment? La réponse est simplement de créer un nouveau nombre appelé
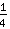
(lire: un quart). Si tu veux imaginer combien cela coûte, il suffit de dessiner un gâteau et de le diviser en quatre morceaux.
Et qu'est-ce qu'une telle fraction?
Ce que nous venons de faire avec le gâteau, peut être fait avec chaque nombre: imaginez que vous voulez diviser deux nombres, mais ce n'est pas possible. Alors, vous venez de composer un nouveau numéro qui sera le résultat de cette division. Donc, la



ne signifie rien d'autre que le résultat de
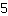
divisé par
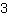
. Le nombre dessus est appelé numérateur, ainsi que celui dessous dénominateur. Alors,
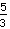
a pour numérateur
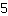
et dénominateur
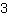
.
Et comment calculer avec de telles fractions?
Gardez d'abord à l'esprit: Il existe différentes fractions qui décrivent le même nombre. Par exemple,
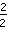
et
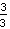
sont tous deux identiques à

, parce que
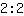
et
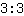
donnent tous les deux

. Nous avons donc deux fractions d'apparence différentes mais décrivant le même nombre. Transformer une fraction dans une autre qui décrit le même nombre s'appelle agrandissement ou réduction d'une fraction.
Par ailleurs, si vous voulez ajouter ou soustraire des fractions, vous devez les mettre sur le même dénominateur. Ceci peut être fait en trouvant le plus petit commun multiple (PPCM) des dénominateurs.
Par contre, si vous voulez multiplier les fractions, multipliez simplement les numérateurs et les dénominateurs. Pour diviser les fractions, échanger le numérateur et le dénominateur de la fraction que vous souhaitez diviser, puis multipliez ces fractions.
Comment appelle-t-on l'ensemble des nombres contenant des fractions?
Ce sont les nombres rationnels, indiqué par Q.