Qu'est-ce qu'un point tournant?
Un point tournant est un point où le graphique d'une fonction a la valeur la plus élevée localement (appelée point tournant maximal) ou la valeur la plus faible localement (appelée point tournant minimal). Une fonction ne doit cependant pas avoir leurs valeurs les plus élevées et les plus basses dans les points tournant.
Ce graphique, par exemple a un point tournant maximal à
|
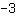
tandis que la fonction a des valeurs plus élevées, par ex. dans
|
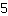
. Cela implique qu'un point tournant maximal n'est pas la valeur la plus élevée de la fonction, mais juste localement la plus élevée, c'est-à-dire qu'il n'y a pas de valeur supérieure au moins dans le voisinage de ce point.
Comment trouver des points tournants?
Étant donné que les tangentes dans un point tournant sont horizontales, c'est-à-dire qu'elles ont une pente de
,
alors l'idée de base est la suivante:
- trouver un moyen de calculer les pentes des tangentes, possible par dérivation.
- Par conséquent on peut trouver quand la pente de la tangente est . Voir donc s'il pourrait être un point tournant.
Cela signifie que pour trouver des points tournants on doit rechercher les racines de la dérivation.
La pente implique-t-elle toujours un tournant?
Non. Si la pente est de
, nous avons au maximum un point tournant maximal (illustré ci-dessus),
un point tournant minimal
ou la pente devient juste
pendant un moment bien que vous n'ayez pas de point tournant. Un tel point est appelé point d'inflexion horizontal, ou simplement point d'inflexion. Puisque la pente de la fonction est toujours
dans ces trois points, ils prennent le nom de points stationnaires.
La pente doit-elle toujours être dans les points tournant?
Oui. C'est juste. Mais pas la réversion, comme vu ci-dessus. Nous disons donc: avoir une pente
est condition nécessaire mais pas suffisant pour avoir un point tournant.
Supposons que nous avons la pente . Comment puis-je savoir si j'ai un point tournant maximal / minimal ou un point d'inflexion?
En utilisant le critère de changement du signe avec la dérivée première et deuxième c'est possible.
Je dois trouver des point tournant comme devoirs et je ne sais pas comment. Que puis-je faire?
Entrez simplement votre fonction ci-dessus. Mathepower fait le calcul, avec les explications et tous les passages.