Cos'è una funzione lineare?
Una funzione lineare è una funzione il cui grafico è una retta. Ecco un esempio:
Il tuo esercizio: 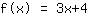
Qui vedi il grafico della tua funzione.
|
|
- Zeri in -1.333
- Intersezione con l'asse y in (0|4)
|
Il grafico di una funzione lineare è sempre una retta.
In algebra lineare una funzione lineare è più comunemente chiamata trasformazione lineare.
Cos'è la pendenza di una funzione lineare?
La pendenza di una funzione lineare rappresenta il coefficiente della variabile x e indica di quante unità ci si sposta lungo l'asse delle y per uno spostamento unitario lungo x. Esempio:
Il tuo esercizio: 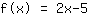
Qui vedi il grafico della tua funzione.
|
|
- Zeri in 2.5
- Intersezione con l'asse y in (0|-5)
|
Come vediamo, questa funzione ha pendenza
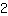
. se ci si sposta di un'unità verso destra, allora il valore delle y aumenta di
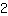
.
Un altro esempio, questa volta con pendenza negativa:
Il tuo esercizio: 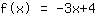
Qui vedi il grafico della tua funzione.
|
|
- Zeri in 1.333
- Intersezione con l'asse y in (0|4)
|
Questa funzione lineare ha pendenza
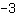
. Ciò significa che, andando verso destra di un'unità, ci si sposta verso di tre unità in modo decrescente lungo y.
Cos'è l'intersezione con l'asse delle y?
L'intersezione con l'asse delle y è il termine noto nella funzione lineare e indica dove si interseca la funzione con l'asse y (come dice il nome stesso). Osservando le due funzioni di prima, si vede come
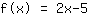
interseca l'asse y in
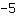
e
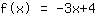
interseca l'asse y in
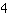
.
Come si trova l'equazione della funzione lineare dati la sua pendenza e un punto di appartenenza?
Basta inserire il punto nell'equazione della retta. Cioè sostituire le coordinate del punto al posto di x e f(x). Facciamo un esempio: come dati sappiamo che la funzione ha pendenza
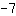
e passa per il punto (-2|5).
Il tuo esercizio:
Punto (-2|5); Pendenza -7;
Il tuo esercizio: 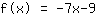
Qui vedi il grafico della tua funzione.
|
|
- Zeri in -1.286
- Intersezione con l'asse y in (0|-9)
Mathepower ha calcolato come segue:
Calcolo dell'intersezione con l'asse y:
Formula generica della funzione lineare: f(x)=mx+b
Inserisci 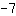 in m, in m, 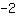 in x e in x e 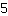 al posto di f(x). al posto di f(x).
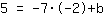 | | | Moltiplichiamo 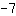 per per 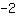 |
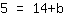 | | | Scambiamo di posizione i membri dell'equazione. |
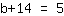 | | | 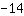 |
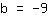 | | |
Allora l'intersezione con l'asse delle y è 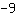
L'equazione della funzione è quindi: 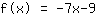
|
Come si trova l'equazione della funzione lineare passante per due punti?
In questo caso si può facilmente calcolare la pendenza m, sapendo che si può calcolare dalle coordinate dei punti. Infatti, m =
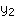
-
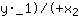
-
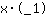
, cioè la pendenza è data dalla distanza dei due punti lungo y diviso la distanza lungo x. Vediamo un esempio:
Il tuo esercizio:
Punto (1|2); Punto (3|8);
Il tuo esercizio: 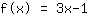
Qui vedi il grafico della tua funzione.
|
|
- Zeri in 0.333
- Intersezione con l'asse y in (0|-1)
Mathepower ha calcolato come segue:
Calcolo della pendenza m: si usa la formula 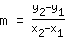 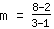 | | | Sommiamo  a a 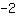 |
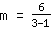 | | | Sommiamo 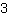 a a 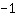 |
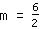 | | | Dividiamo 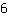 per per 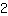 |
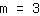 | | |
Calcolo dell'intersezione con l'asse y:
Formula generica della funzione lineare: f(x)=mx+b
Inserisci 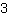 in m, in m, 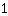 in x e in x e 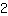 al posto di f(x). al posto di f(x).
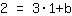 | | |
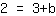 | | | Scambiamo di posizione i membri dell'equazione. |
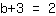 | | | 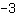 |
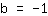 | | |
Allora l'intersezione con l'asse delle y è 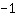
L'equazione della funzione è quindi: 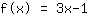
|
Come si può vedere, si è calcolata la pendenza. Adesso, per trovare l'equazione della funzione ci si riconduce al caso precedente: bisogna inserire un punto nell'equazione della retta e trovare il termine noto q, intersezione con l'asse delle y.
Posso vedere un altro esempio?
Certo, inserisci un tuo esercizio qui sopra e sarà risolto. Questa è l'idea di Mathepower:
non impari solo vedendo delle spiegazioni già preparate, ma hai la possibilità di vedere i tuoi stessi esercizi spiegati.