A cosa serve il metodo delle derivate successive?
Esso serve a vedere se una funzione, la cui derivata prima in un punto è
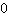
, ha in quel punto un massimo, un minimo o un punto di flesso a tangente orizzontale. Vediamo qui tre esempi in cui la funzione ha derivata nulla in (1|2):
Questa funzione ha in (1|2) un punto di massimo. In
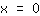
il grafico è crescente, cioè ha derivata positiva, mentre in
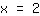
è decrescente, cioè ha derivata negativa. Data una funzione con un massimo in un punto allora il segno della derivata è + in un intorno sinistro del punto e - in un suo intorno destro. La derivata ha un cambio di segno da + a -.
Questa funzione ha in (1|2) un punto di minimo. In
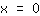
il grafico è decrescente, cioè ha derivata negativa, mentre in
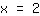
è crescente, cioè ha derivata positiva. Data una funzione con un minimo in un punto allora il segno della derivata è - in un intorno sinistro del punto e + in un suo intorno destro. La derivata ha un cambio di segno da - a +.
Anche questa funzione ha in (1|2) la derivata prima uguale a
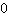
. Tuttavia si può vedere che sia in
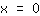
che in
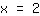
la funzione è crescente. Se la derivata prima non cambia segno nell'intorno del punto significa che esso non è un punto estremante (massimo o minimo). Un punto del genere è detto punto di flesso a tangente orizzontale.
Come si usa il metodo delle derivate successive?
- Si inizia calcolando la derivata prima della tua funzione.
- Poi si calcolano gli zeri della derivata prima, cioè i punti stazionari della tua funzione .
- Infine si studia il segno della derivata prima (ponendo la funzione
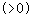. In questo modo si trovano gli intervalli un cui è positiva o negativa. Se la derivata cambia segno nell'intorno di uno zero, si ha un punto estremante, altrimenti no. Perché il metodo delle derivate successive è detto criterio sufficiente?
Che la derivata prima in un punto sia 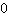è condizione necessaria per trovare un punto estremante, ma non è sufficiente. Cioè che se si ha pendenza 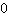in un punto, non è detto che esso sia un punto di massimo o minimo (si veda il punto di flesso orizzontale qui sopra).
Se la derivata prima è 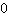in un punto e cambia segno nel suo intorno, allora si tratta di un punto estremante. Si dice che la derivata prima nulla in un punto e il suo cambio di segno in un intorno del punto sono condizione sufficiente per poter avere un punto estremante.
Posso vedere un altro esempio?
Certo, Mathepower è qui per questo. Inserisci pure una funzione e Mathepower troverà i suoi punti stazionari.