Come si sommano o sottraggono le frazioni?
Nel caso più semplice le frazioni hanno lo stesso denominatore, allora basta sommare i numeratori tra di loro.
Esempio:
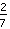
+
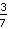
=
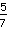
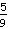
-
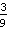
=
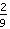
E così via.
E quando le frazioni non hanno lo stesso denominatore?
È necessario allora trovare un comune denominatore tramite la scomposizione in fattori primi. In tal modo è possibile calcolare il minimo comune multiplo (mcm) per entrambi i denominatori. O semplicemente si può trovare un numero divisibile per entrambi i denominatori.
Esempio: si voglia calcolare
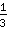
+
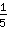
. Un possibile denominatore comune può essere
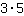
=
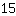
. Allora si calcola:
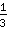
+
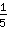
=
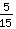
+
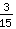
=
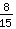
.
Un altro esempio: si voglia calcolare
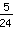
-
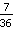
. Si potrebbe anche usare
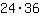
=

, tuttavia si nota che, dopo uno sguardo più attento, esiste anche un multiplo comune più piccolo. In questo caso
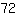
, che è proprio il mcm. Allora si può calcolare:
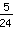
-
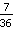
=
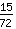
-
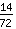
=
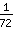
.
Se vorresti vedere ancora altri esempi, inserisci pure un tuo esercizio nella calcolatrice qui sopra… sarà calcolato subito e gratuitamente.