La ricostruzione di funzioni dal grafico


Si cerca la funzione

Grado della funzione:
1 2 3 4 5

( Il grado è il più alto esponente della x. )


Simmetrie:
simmetrica rispetto all'asse y
simmetrica rispetto all'origine


Intersezione con l'asse y



Zeri / massimi / minimi / punti di flesso:
in x=
in x=
in x=
in x=
in x=


Punti caratteristici:
in |)
in |)
in |)
in (|)
in (|)


Pendenza nei punti:
Pendenza in x=
Pendenza in x=
Pendenza in

Cosa sono gli esercizi di ricostruzione?

Gli esercizi di ricostruzione sono l'opposto dello studio di funzione. Nello studio di funzione si ha una funzione data e si cercano gli zeri, i punti stazionari e critici. In un esercizio di ricostruzione si hanno dei dati del grafico della funzione e si cerca la funzione che rispetta queste condizioni.

Come si ricostruisce una funzione?

Per prima cosa si trovano le equazioni e si risolvono. Questo permette di ottenere i coefficienti della funzione. Ecco un esempio: Si voglia trovare una funzione di terzo grado che ha un minimo nel punto (1|-4) e un massimo in (-1|3).


Stiamo cercando una funzione del tipo:
funzione quadratica
punto di massimo in (-1|3)
punto di minimo in (1|-4)

Mathepower ha trovato la seguente funzione:
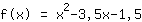
1*f(x)=1*x^2+-3.5*x+-1.5
Qui vedi il grafico della tua funzione.
Dein Browser unterstützt den HTML-Canvas-Tag nicht. Hol dir einen neuen. :P
  • Zeri in -0.386; 3.886
  • Intersezione con l'asse y in (0|-1.5)
  • massimi/minimi in (1.75|-4.563)
  • Punti di flesso obliqui

Mathepower ha così calcolato:
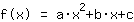
f(x)=1*a*x^2+1*b*x+1*c
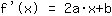
f'(x)=2*a*x+1*b
f''(x)=2*a

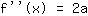
Il punto (-1|3) porta all'equazione :
f(-1)=3
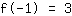
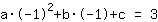
1*a*-1^2+1*b*-1+1*c=3
semplificato :
1a-1b+1c=3

Il punto (1|-4) porta all'equazione :
f(1)=-4
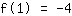
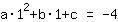
1*a*1^2+1*b*1+1*c=-4
semplificato :
1a+1b+1c=-4

In totale si ottiene il seguente sistema di equazioni :
  a   -1b   +c    = 3 
  a   +b   +c    = -4 

Il sistema di equazioni si risolve così:
  a   -1b   +c    = 3 
  a   +b   +c    = -4 
  a   -1b   +c    = 3 
     2b       = -7 
 ( -1 volte l'equazione 1 è stata sommata all'equazione 2 )
  a   -1b   +c    = 3 
     b       = -3,5 
 ( L'equazione 2 è stata divisa per 2 )

2 ° equazione: b+0c = -3,5
c è scelto opportunamente
Si risolve per b : :   b = 0c -3,5

1 ° equazione:
a  -1b  +c   =  3
Si sostituiscono le variabili già calcolate:   
a  -1⋅(0c -3,5)  +⋅1c    =  3
Si risolve per a : a = -1c -0,5
Poniamo a uguale a 1.
Significa che c è uguale a -1,5

Sostituendo si vede che la funzione è uguale a 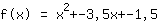f(x)=1*1*x^2+1*-3.5*x+1*-1.5 ist.



Come si trova una funzione dati dei punti?

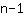
La regola generale è che per n punti esiste sempre una funzione di grado n-1 passante per essi. È quindi facile trovare una funzione ad esempio di terzo grado passante per i quattro punti (-1|3), (0|2), (1|1) e (2|4):


Stiamo cercando una funzione del tipo:
funzione di grado 3
Il punto in (-1|3)
Il punto in (0|2)
Il punto in (1|1)
Il punto in (2|4)

Mathepower ha trovato la seguente funzione:
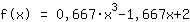
1*f(x)=0.667*x^3+-1.667*x+2
Qui vedi il grafico della tua funzione.
Dein Browser unterstützt den HTML-Canvas-Tag nicht. Hol dir einen neuen. :P
  • Zeri in -2
  • Intersezione con l'asse y in (0|2)
  • massimi/minimi in (-0.913|3.014); (0.913|0.986)
  • Punti di flesso obliqui in (0|2)

Mathepower ha così calcolato:
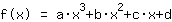
f(x)=1*a*x^3+1*b*x^2+1*c*x+1*d
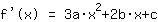
f'(x)=3*a*x^2+2*b*x+1*c
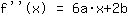
f''(x)=6*a*x+2*b

Il punto (-1|3) porta all'equazione :
f(-1)=3
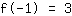
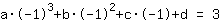
1*a*-1^3+1*b*-1^2+1*c*-1+1*d=3
semplificato :
-1a+1b-1c+1d=3

Il punto (0|2) porta all'equazione :
f(0)=2
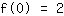
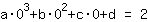
1*a*0^3+1*b*0^2+1*c*0+1*d=2
semplificato :
0a+0b+0c+1d=2

Il punto (1|1) porta all'equazione :
f(1)=1
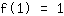
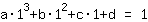
1*a*1^3+1*b*1^2+1*c*1+1*d=1
semplificato :
1a+1b+1c+1d=1

Il punto (2|4) porta all'equazione :
f(2)=4
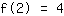
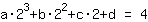
1*a*2^3+1*b*2^2+1*c*2+1*d=4
semplificato :
8a+4b+2c+1d=4

In totale si ottiene il seguente sistema di equazioni :
  -1a   +b   -1c   +d    = 3 
           d    = 2 
  a   +b   +c   +d    = 1 
  8a   +4b   +2c   +d    = 4 

Il sistema di equazioni si risolve così:
  -1a   +b   -1c   +d    = 3 
           d    = 2 
  a   +b   +c   +d    = 1 
  8a   +4b   +2c   +d    = 4 
  -1a   +b   -1c   +d    = 3 
           d    = 2 
  a   +b   +c   +d    = 1 
     -4b   -6c   -7d    = -4 
 ( -8 volte l'equazione 3 è stata sommata all'equazione 4 )
  -1a   +b   -1c   +d    = 3 
           d    = 2 
     2b      +2d    = 4 
     -4b   -6c   -7d    = -4 
 ( 1 volte l'equazione 1 è stata sommata all'equazione 3 )
  a   -1b   +c   -1d    = -3 
           d    = 2 
     2b      +2d    = 4 
     -4b   -6c   -7d    = -4 
 ( L'equazione 1 è stata divisa per -1 )
  a   -1b   +c   -1d    = -3 
           d    = 2 
     2b      +2d    = 4 
        -6c   -3d    = 4 
 ( 2 volte l'equazione 3 è stata sommata all'equazione 4 )
  a   -1b   +c   -1d    = -3 
     2b      +2d    = 4 
           d    = 2 
        -6c   -3d    = 4 
 ( l'equazione 3 è stata scambiata con l'equazione 2 )
  a   -1b   +c   -1d    = -3 
     b      +d    = 2 
           d    = 2 
        -6c   -3d    = 4 
 ( L'equazione 2 è stata divisa per 2 )
  a   -1b   +c   -1d    = -3 
     b      +d    = 2 
        -6c   -3d    = 4 
           d    = 2 
 ( l'equazione 4 è stata scambiata con l'equazione 3 )
  a   -1b   +c   -1d    = -3 
     b      +d    = 2 
        c   +0,5d    = -0,667 
           d    = 2 
 ( L'equazione 3 è stata divisa per -6 )


4 ° equazione:
      d   =  2

3 ° equazione:
    c  +0,5d   =  -0,667
Si sostituiscono le variabili già calcolate:   
    c  +0,5⋅2   =  -0,667
Si risolve per c : c = -1,667

2 ° equazione:
  b    +d   =  2
Si sostituiscono le variabili già calcolate:   
  b    +⋅2   =  2
Si risolve per b : b = 0

1 ° equazione:
a  -1b  +c  -1d   =  -3
Si sostituiscono le variabili già calcolate:   
a  -1⋅0  +⋅(-1,667)  -1⋅2   =  -3
Si risolve per a : a = 0,667

Sostituendo si vede che la funzione è uguale a 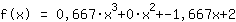f(x)=1*0.667*x^3+1*0*x^2+1*-1.667*x+1*2 ist.



Ma come si trova una funzione dato un punto di flesso?

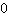
Poiché è data una condizione in più, cioè il punto di flesso, si ottengono più equazioni: la prima è l'appartenenza del punto all'equazione della funzione, la seconda è l'appartenenza del punto alla derivata prima, che deve dare 0. Qui vediamo un esempio di funzione di terzo grado che ha un punto di flesso in (1|3):


Stiamo cercando una funzione del tipo:
funzione di grado 3
zero in 2
zero in 4
punto di flesso obliquo in (1|3)

Mathepower ha trovato la seguente funzione:
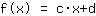
1*f(x)=1*c*x+1*d
Qui vedi il grafico della tua funzione.
Dein Browser unterstützt den HTML-Canvas-Tag nicht. Hol dir einen neuen. :P
  • Zeri
  • Intersezione con l'asse y in (0|0)
  • massimi/minimi
  • Punti di flesso obliqui

Mathepower ha così calcolato:
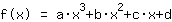
f(x)=1*a*x^3+1*b*x^2+1*c*x+1*d
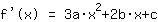
f'(x)=3*a*x^2+2*b*x+1*c
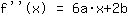
f''(x)=6*a*x+2*b

Il punto (1|3) porta all'equazione :
f(1)=3
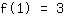
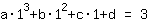
1*a*1^3+1*b*1^2+1*c*1+1*d=3
semplificato :
1a+1b+1c+1d=3

In totale si ottiene il seguente sistema di equazioni :
  a   +b   +c   +d    = 3 

Il sistema di equazioni si risolve così:
  a   +b   +c   +d    = 3 

1 ° equazione: c+1d = 3
d è scelto opportunamente
Si risolve per c : :   c = -1d +3

Sostituendo si vede che la funzione è uguale a 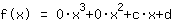f(x)=1*0*x^3+1*0*x^2+1*c*x+1*d ist.



Como posso applicare questo al mio esercizio?

Inserisci pure il tuo esercizio qui sopra e Mathepower ti mostra come risolverlo, oppure inventalo semplicemente e osserva cosa fa Mathepower.