Cos'è lo studio di funzione?
Per studio di funzione si intende trovare dei punti caratteristici di una funzione, come le intersezioni con l'asse y, con l'asse x (cioè gli zeri o radici), i massimi, i minimi e i punti di flesso, per poterla descrivere.
Come si trovano questi punti?
Si inizia calcolando le prime tre derivate della funzione. Poi si trovano gli zeri della funzione come anche delle derivate. Gli zeri sono soluzioni dell'equazione
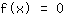
. I punti estremanti si trovano solo negli zeri della funzione, cioè bisogna risolvere l'equazione
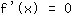
per trovare gli eventuali punti estremanti. In un punto di flesso la derivata seconda deve essere uguale a
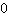
, cioè bisogna risolvere l'equazione
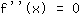
(per vedere se uno zero della derivata è un punto stazionario, e che tipo è, si può utilizzare il criterio delle derivate successive).
Perché nelle scuole lo studio di funzione non è così tanto approfondito?
È un po' inutile se si pensa che bisogna fare calcoli senza capire ciò che si sta facendo. Per questo oggigiorno si incontrano esercizi in cui si deve ragionare sul tipo di punti che si stanno considerando, piuttosto che semplicemente doverli calcolare.
Posso vedere un esempio?
Certo, vediamo lo studio della seguente funzione
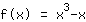
.
Mathepower lavora con questa funzione:
Qui vedi il grafico della tua funzione.
|
|
- Zeri in -1; 0; 1
- Intersezione con l'asse y in (0|0)
- massimi/minimi in (-0.577|0.385); (0.577|-0.385)
- Punti di flesso obliqui in (0|0)
Mathepower ha calcolato come segue:
Punti stazionari:
Si estraggono le radici da 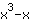
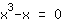 | | | Si estrae la  . . |
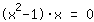 | | | 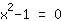 | | | Legge di annullamento del prodotto: o il fattore 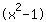 è nullo… è nullo… |
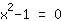 | | | +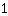 |
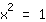 | | | Si applica la radice quadrata a entrambi i membri dell'equazione. |
 | | |  | | | Estraiamo la radice quadrata di 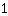 |
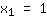 | | |  | | | Estraiamo la radice quadrata di 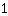 |
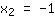 | | | 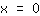 | | | … o il fattore 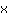 è nullo è nullo |
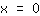 | | |
I punti stazionari sono i seguenti: {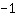 ; ;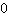 ; ;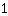 } }
Simmetria:
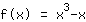 è simmetrica rispetto all'origine. è simmetrica rispetto all'origine.
Intersezione con l'asse delle ascisse: si eguaglia la funzione a 0
Si inserisce 0 nella funzione 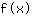 : :
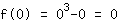
Allora l'intersezione con l'asse delle y è (0|0)
Si deriva la funzione 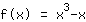
| Si deriva la funzione 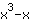 : : | ( Derivata di  ) ) | + | ( Derivata di 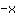 ) ) | 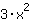 | + | 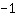 |
La derivata di 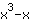 è allora è allora 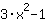 . . |
| |
|
La derivata prima è la seguente: 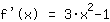
La derivata seconda, cioè la derivata della funzione, è: 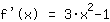 : :
| Si deriva la funzione 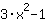 : : | ( Derivata di 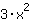 ) ) | + | ( Derivata di 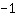 ) ) | 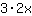 | + | 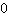 |
La derivata di 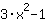 è allora è allora 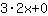 . . |
| |
|
Semplificazione della derivata:
La derivata seconda è la seguente: 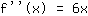
La derivata terza, cioè la derivata della funzione, è: 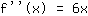 : :
La derivata di 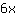 è è 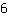
La derivata terza è la seguente: 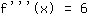
Si cercano i punti estremanti.
Criterio importante: trovare gli zeri della derivata prima.
Si estraggono le radici da 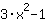
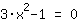 | | | +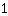 |
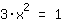 | | | : 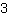 |
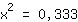 | | | Si applica la radice quadrata a entrambi i membri dell'equazione. |
 | | |  | | | Estraiamo la radice quadrata di  |
 | | |  | | | Estraiamo la radice quadrata di  |
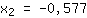 | | |
Probabili punti stazionari in: {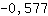 ; ;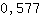 } }
Si inseriscono gli zeri della derivata prima nella derivata seconda:
Si inserisce -0.577 nella funzione 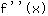 : :
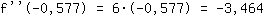
-3.464 che è minore di 0. Allora in 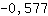 è presente un massimo. è presente un massimo.
Si inserisce -0.577 nella funzione 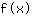 : :
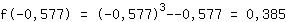
punto di massimo (-0.577|0.385)
Si inserisce 0.577 nella funzione 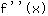 : :

3.464 che è maggiore di 0. Allora in 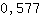 è presente un minimo. è presente un minimo.
Si inserisce 0.577 nella funzione 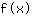 : :
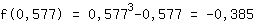
punto di minimo (0.577|-0.385)
Si cercano i punti di flesso obliqui
Criterio importante: trovare gli zeri della derivata seconda.
Si estraggono le radici da 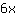
Probabili punti di flesso obliqui in {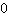 } }
Si inseriscono gli zeri della derivata seconda nella derivata terza:
Poiché nella derivata terza la variabile x non è più presente, l'inserimento dello zero risulta in 6
6 è maggiore di 0. Allora in 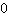 è presente un punto di flesso obliquo ascendente (concavità in basso -> alto). è presente un punto di flesso obliquo ascendente (concavità in basso -> alto).
Si inserisce 0 nella funzione 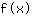 : :
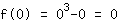
punto di flesso obliquo (0|0)
|