Qui alcuni esempi su come moltiplicare le frazioni.
Iniziamo con un esempio di base: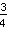 
* 
.
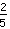Basta moltiplicare i numeratori e i denominatori tra di loro e il gioco è fatto:
* = 
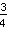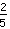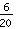
E infine semplificare: =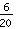 
.
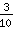A proposito, è importante tenere a mente e non confondersi che: quando si moltiplicano o dividono frazioni, sia il numeratore che il denominatore ne sono affetti e, invece, quando si sommano o sottraggono il denominatore rimane uguale (una volta che si è posto uguale al mcm)!
Prossimo esempio: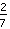 
* 
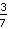
Anche se i denominatori sono uguali, nella moltiplicazione bisogna moltiplicare numeratore con numeratore e denominatore con denominatore.
* = 
.
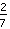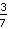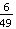Un altro esempio: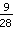 
* 
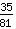
In questo caso si lavorerebbe con numeri molto grandi. Ciò può essere evitato semplificando in croce. Infatti,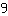 
e 
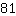si semplificano perché divisione e prodotto sono operazioni con stessa priorità.
* = 
* 
.
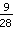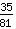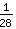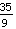Un'altra semplificazione si può fare tra il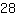 
e il 
, divisibili per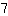 
:
* = 
* 
= 
.
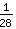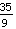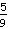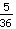Nonostante all'inizio l'esercizio sembrasse difficile, in fin dei conti si sono moltiplicati sono numeri piccoli.
Molto importante: Questa semplificazione in croce vale solo per la moltiplicazione e divisione! Nel caso di una somma o sottrazione non è possibile farlo perché risulterebbe sbagliato.
Vediamo il seguente esempio:
: 
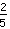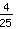
Quando si dividono due frazioni, si procede con la risoluzione moltiplicando per l'inverso della seconda frazione:
: = * 
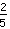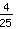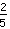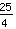
e adesso si può semplificare in croce:
* = 
* 
= 
* 
=
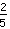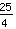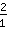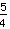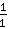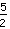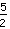
allora la soluzione è 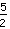oppure 
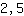se scritto come numero decimale.
Se vuoi vedere altri esempi, inserisci pure altri esercizi. Mathepower ne calcolerà subito la soluzione.